scipy.stats.nbinom#
- scipy.stats.nbinom = <scipy.stats._discrete_distns.nbinom_gen object>[source]#
A negative binomial discrete random variable.
As an instance of the
rv_discreteclass,nbinomobject inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.See also
Notes
Negative binomial distribution describes a sequence of i.i.d. Bernoulli trials, repeated until a predefined, non-random number of successes occurs.
The probability mass function of the number of failures for
nbinomis:\[f(k) = \binom{k+n-1}{n-1} p^n (1-p)^k\]for \(k \ge 0\), \(0 < p \leq 1\)
nbinomtakes \(n\) and \(p\) as shape parameters where \(n\) is the number of successes, \(p\) is the probability of a single success, and \(1-p\) is the probability of a single failure.Another common parameterization of the negative binomial distribution is in terms of the mean number of failures \(\mu\) to achieve \(n\) successes. The mean \(\mu\) is related to the probability of success as
\[p = \frac{n}{n + \mu}\]The number of successes \(n\) may also be specified in terms of a “dispersion”, “heterogeneity”, or “aggregation” parameter \(\alpha\), which relates the mean \(\mu\) to the variance \(\sigma^2\), e.g. \(\sigma^2 = \mu + \alpha \mu^2\). Regardless of the convention used for \(\alpha\),
\[\begin{split}p &= \frac{\mu}{\sigma^2} \\ n &= \frac{\mu^2}{\sigma^2 - \mu}\end{split}\]This distribution uses routines from the Boost Math C++ library for the computation of the
pmf,cdf,sf,ppf,isfandstatsmethods. [1]The probability mass function above is defined in the “standardized” form. To shift distribution use the
locparameter. Specifically,nbinom.pmf(k, n, p, loc)is identically equivalent tonbinom.pmf(k - loc, n, p).References
[1]The Boost Developers. “Boost C++ Libraries”. https://www.boost.org/.
Examples
>>> import numpy as np >>> from scipy.stats import nbinom >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1)
Calculate the first four moments:
>>> n, p = 5, 0.5 >>> mean, var, skew, kurt = nbinom.stats(n, p, moments='mvsk')
Display the probability mass function (
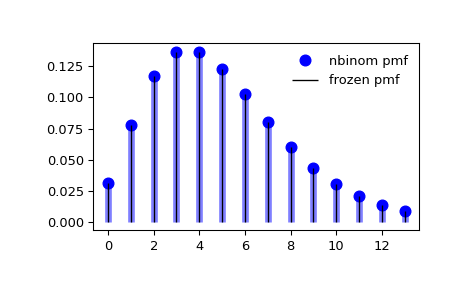
pmf):>>> x = np.arange(nbinom.ppf(0.01, n, p), ... nbinom.ppf(0.99, n, p)) >>> ax.plot(x, nbinom.pmf(x, n, p), 'bo', ms=8, label='nbinom pmf') >>> ax.vlines(x, 0, nbinom.pmf(x, n, p), colors='b', lw=5, alpha=0.5)
Alternatively, the distribution object can be called (as a function) to fix the shape and location. This returns a “frozen” RV object holding the given parameters fixed.
Freeze the distribution and display the frozen
pmf:>>> rv = nbinom(n, p) >>> ax.vlines(x, 0, rv.pmf(x), colors='k', linestyles='-', lw=1, ... label='frozen pmf') >>> ax.legend(loc='best', frameon=False) >>> plt.show()
Check accuracy of
cdfandppf:>>> prob = nbinom.cdf(x, n, p) >>> np.allclose(x, nbinom.ppf(prob, n, p)) True
Generate random numbers:
>>> r = nbinom.rvs(n, p, size=1000)
Methods
rvs(n, p, loc=0, size=1, random_state=None)
Random variates.
pmf(k, n, p, loc=0)
Probability mass function.
logpmf(k, n, p, loc=0)
Log of the probability mass function.
cdf(k, n, p, loc=0)
Cumulative distribution function.
logcdf(k, n, p, loc=0)
Log of the cumulative distribution function.
sf(k, n, p, loc=0)
Survival function (also defined as
1 - cdf, but sf is sometimes more accurate).logsf(k, n, p, loc=0)
Log of the survival function.
ppf(q, n, p, loc=0)
Percent point function (inverse of
cdf— percentiles).isf(q, n, p, loc=0)
Inverse survival function (inverse of
sf).stats(n, p, loc=0, moments=’mv’)
Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(n, p, loc=0)
(Differential) entropy of the RV.
expect(func, args=(n, p), loc=0, lb=None, ub=None, conditional=False)
Expected value of a function (of one argument) with respect to the distribution.
median(n, p, loc=0)
Median of the distribution.
mean(n, p, loc=0)
Mean of the distribution.
var(n, p, loc=0)
Variance of the distribution.
std(n, p, loc=0)
Standard deviation of the distribution.
interval(confidence, n, p, loc=0)
Confidence interval with equal areas around the median.