scipy.special.spence#

scipy.special.spence(z, out=None) = <ufunc 'spence'>#

Spence’s function, also known as the dilogarithm.

It is defined to be

$$\int_1^z \frac{\log(t)}{1 - t}dt$$

for complex $z$, where the contour of integration is taken to avoid the branch cut of the logarithm. Spence’s function is analytic everywhere except the negative real axis where it has a branch cut.

Parameters:

zarray_like

Points at which to evaluate Spence’s function

outndarray, optional

Optional output array for the function results

Returns:

sscalar or ndarray

Computed values of Spence’s function

Notes

There is a different convention which defines Spence’s function by the integral

$$-\int_0^z \frac{\log(1 - t)}{t}dt;$$

this is our spence(1 - z).

Examples

Try it in your browser!

>>> import numpy as np
>>> from scipy.special import spence
>>> import matplotlib.pyplot as plt

The function is defined for complex inputs:

>>> spence([1-1j, 1.5+2j, 3j, -10-5j])
array([-0.20561676+0.91596559j, -0.86766909-1.39560134j,
       -0.59422064-2.49129918j, -1.14044398+6.80075924j])

For complex inputs on the branch cut, which is the negative real axis, the function returns the limit for z with positive imaginary part. For example, in the following, note the sign change of the imaginary part of the output for z = -2 and z = -2 - 1e-8j:

>>> spence([-2 + 1e-8j, -2, -2 - 1e-8j])
array([2.32018041-3.45139229j, 2.32018042-3.4513923j ,
       2.32018041+3.45139229j])

The function returns nan for real inputs on the branch cut:

>>> spence(-1.5)
nan

Verify some particular values: spence(0) = pi**2/6, spence(1) = 0 and spence(2) = -pi**2/12.

>>> spence([0, 1, 2])
array([ 1.64493407,  0.        , -0.82246703])
>>> np.pi**2/6, -np.pi**2/12
(1.6449340668482264, -0.8224670334241132)

Verify the identity:

spence(z) + spence(1 - z) = pi**2/6 - log(z)*log(1 - z)

>>> z = 3 + 4j
>>> spence(z) + spence(1 - z)
(-2.6523186143876067+1.8853470951513935j)
>>> np.pi**2/6 - np.log(z)*np.log(1 - z)
(-2.652318614387606+1.885347095151394j)

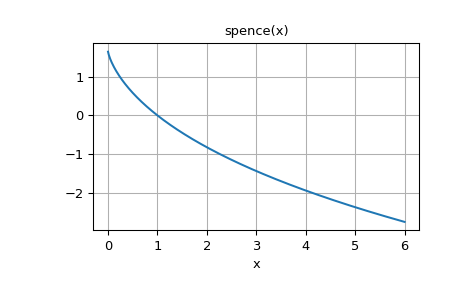
Plot the function for positive real input.

>>> fig, ax = plt.subplots()
>>> x = np.linspace(0, 6, 400)
>>> ax.plot(x, spence(x))
>>> ax.grid()
>>> ax.set_xlabel('x')
>>> ax.set_title('spence(x)')
>>> plt.show()

Go BackOpen In Tab