scipy.special.jvp#

scipy.special.jvp(v, z, n=1)[source]#

Compute derivatives of Bessel functions of the first kind.

Compute the nth derivative of the Bessel function Jv with respect to z.

Parameters:

varray_like or float: Order of Bessel function
zcomplex: Argument at which to evaluate the derivative; can be real or complex.
nint, default 1: Order of derivative. For 0 returns the Bessel function jv itself.

Returns:

scalar or ndarray: Values of the derivative of the Bessel function.

Notes

The derivative is computed using the relation DLFM 10.6.7 [2].

References

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

[2]

NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/10.6.E7

Examples

Compute the Bessel function of the first kind of order 0 and its first two derivatives at 1.

>>> from scipy.special import jvp
>>> jvp(0, 1, 0), jvp(0, 1, 1), jvp(0, 1, 2)
(0.7651976865579666, -0.44005058574493355, -0.3251471008130331)

Compute the first derivative of the Bessel function of the first kind for several orders at 1 by providing an array for v.

>>> jvp([0, 1, 2], 1, 1)
array([-0.44005059,  0.3251471 ,  0.21024362])

Compute the first derivative of the Bessel function of the first kind of order 0 at several points by providing an array for z.

>>> import numpy as np
>>> points = np.array([0., 1.5, 3.])
>>> jvp(0, points, 1)
array([-0.        , -0.55793651, -0.33905896])

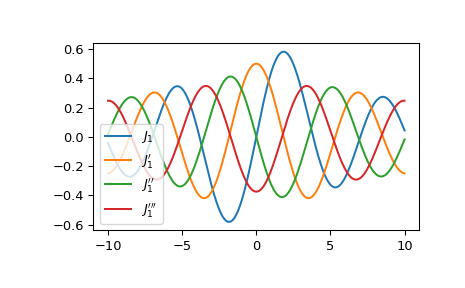
Plot the Bessel function of the first kind of order 1 and its first three derivatives.

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-10, 10, 1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, jvp(1, x, 0), label=r"$J_1$")
>>> ax.plot(x, jvp(1, x, 1), label=r"$J_1'$")
>>> ax.plot(x, jvp(1, x, 2), label=r"$J_1''$")
>>> ax.plot(x, jvp(1, x, 3), label=r"$J_1'''$")
>>> plt.legend()
>>> plt.show()