scipy.special.iti0k0#

scipy.special.iti0k0(x, out=None) = <ufunc 'iti0k0'>#

Integrals of modified Bessel functions of order 0.

Computes the integrals

\[\begin{split}\int_0^x I_0(t) dt \\ \int_0^x K_0(t) dt.\end{split}\]

For more on \(I_0\) and \(K_0\) see i0 and k0.

Parameters:

xarray_like: Values at which to evaluate the integrals.
outtuple of ndarrays, optional: Optional output arrays for the function results.

Returns:

ii0scalar or ndarray: The integral for i0
ik0scalar or ndarray: The integral for k0

References

[1]

S. Zhang and J.M. Jin, “Computation of Special Functions”, Wiley 1996

Examples

Evaluate the functions at one point.

>>> from scipy.special import iti0k0
>>> int_i, int_k = iti0k0(1.)
>>> int_i, int_k
(1.0865210970235892, 1.2425098486237771)

Evaluate the functions at several points.

>>> import numpy as np
>>> points = np.array([0., 1.5, 3.])
>>> int_i, int_k = iti0k0(points)
>>> int_i, int_k
(array([0.        , 1.80606937, 6.16096149]),
 array([0.        , 1.39458246, 1.53994809]))

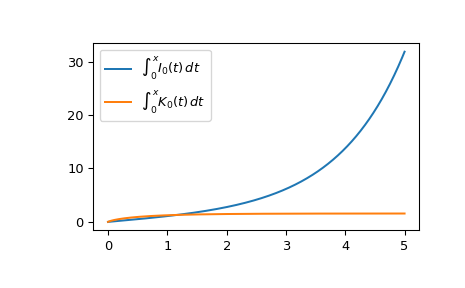
Plot the functions from 0 to 5.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 5., 1000)
>>> int_i, int_k = iti0k0(x)
>>> ax.plot(x, int_i, label=r"$\int_0^x I_0(t)\,dt$")
>>> ax.plot(x, int_k, label=r"$\int_0^x K_0(t)\,dt$")
>>> ax.legend()
>>> plt.show()

../../_images/scipy-special-iti0k0-1.png