scipy.signal.windows.kaiser_bessel_derived

scipy.signal.windows.kaiser_bessel_derived(M, beta, *, sym=True)

Return a Kaiser-Bessel derived window.

Parameters:

Mint

Number of points in the output window. If zero, an empty array is returned. An exception is thrown when it is negative. Note that this window is only defined for an even number of points.

betafloat

Kaiser window shape parameter.

symbool, optional

This parameter only exists to comply with the interface offered by the other window functions and to be callable by get_window. When True (default), generates a symmetric window, for use in filter design.

Returns:

wndarray

The window, normalized to fulfil the Princen-Bradley condition.

See also

kaiser

Notes

It is designed to be suitable for use with the modified discrete cosine transform (MDCT) and is mainly used in audio signal processing and audio coding.

New in version 1.9.0.

References

[1]

Bosi, Marina, and Richard E. Goldberg. Introduction to Digital Audio Coding and Standards. Dordrecht: Kluwer, 2003.

[2]

Wikipedia, “Kaiser window”, https://en.wikipedia.org/wiki/Kaiser_window

Examples

Try it in your browser!

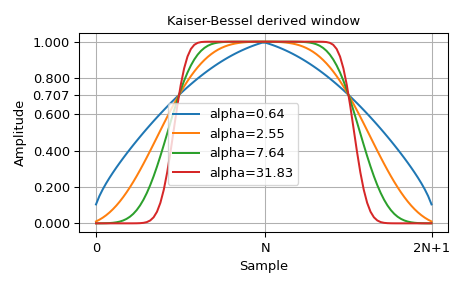
Plot the Kaiser-Bessel derived window based on the wikipedia reference [2]:

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> N = 50
>>> for alpha in [0.64, 2.55, 7.64, 31.83]:
...     ax.plot(signal.windows.kaiser_bessel_derived(2*N, np.pi*alpha),
...             label=f"{alpha=}")
>>> ax.grid(True)
>>> ax.set_title("Kaiser-Bessel derived window")
>>> ax.set_ylabel("Amplitude")
>>> ax.set_xlabel("Sample")
>>> ax.set_xticks([0, N, 2*N-1])
>>> ax.set_xticklabels(["0", "N", "2N+1"])  
>>> ax.set_yticks([0.0, 0.2, 0.4, 0.6, 0.707, 0.8, 1.0])
>>> fig.legend(loc="center")
>>> fig.tight_layout()
>>> fig.show()

Go BackOpen In Tab