scipy.signal.windows.taylor

scipy.signal.windows.taylor(M, nbar=4, sll=30, norm=True, sym=True)

Return a Taylor window.

The Taylor window taper function approximates the Dolph-Chebyshev window’s constant sidelobe level for a parameterized number of near-in sidelobes, but then allows a taper beyond [2].

The SAR (synthetic aperature radar) community commonly uses Taylor weighting for image formation processing because it provides strong, selectable sidelobe suppression with minimum broadening of the mainlobe [1].

Parameters:

Mint

Number of points in the output window. If zero, an empty array is returned. An exception is thrown when it is negative.

nbarint, optional

Number of nearly constant level sidelobes adjacent to the mainlobe.

sllfloat, optional

Desired suppression of sidelobe level in decibels (dB) relative to the DC gain of the mainlobe. This should be a positive number.

normbool, optional

When True (default), divides the window by the largest (middle) value for odd-length windows or the value that would occur between the two repeated middle values for even-length windows such that all values are less than or equal to 1. When False the DC gain will remain at 1 (0 dB) and the sidelobes will be sll dB down.

symbool, optional

When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.

Returns:

outarray

The window. When norm is True (default), the maximum value is normalized to 1 (though the value 1 does not appear if M is even and sym is True).

See also

chebwin, kaiser, bartlett, blackman, hamming, hann

References

[1]

W. Carrara, R. Goodman, and R. Majewski, “Spotlight Synthetic Aperture Radar: Signal Processing Algorithms” Pages 512-513, July 1995.

[2]

Armin Doerry, “Catalog of Window Taper Functions for Sidelobe Control”, 2017. https://www.researchgate.net/profile/Armin_Doerry/publication/316281181_Catalog_of_Window_Taper_Functions_for_Sidelobe_Control/links/58f92cb2a6fdccb121c9d54d/Catalog-of-Window-Taper-Functions-for-Sidelobe-Control.pdf

Examples

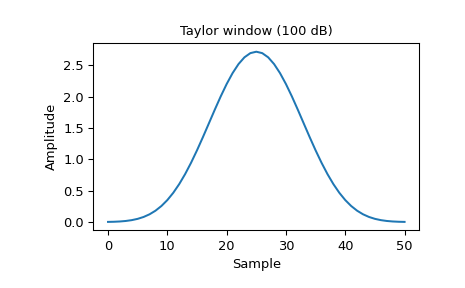
Plot the window and its frequency response:

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.windows.taylor(51, nbar=20, sll=100, norm=False)
>>> plt.plot(window)
>>> plt.title("Taylor window (100 dB)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

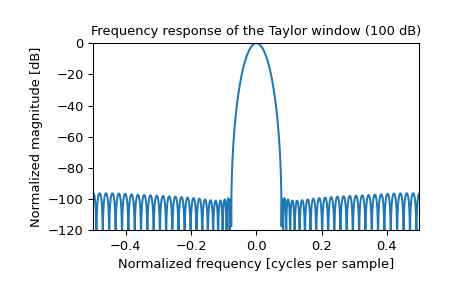
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Taylor window (100 dB)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")