scipy.fft.fft#

scipy.fft.fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)[source]#

Compute the 1-D discrete Fourier Transform.

This function computes the 1-D n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm [1].

Parameters:

xarray_like: Input array, can be complex.
nint, optional: Length of the transformed axis of the output. If n is smaller than the length of the input, the input is cropped. If it is larger, the input is padded with zeros. If n is not given, the length of the input along the axis specified by axis is used.
axisint, optional: Axis over which to compute the FFT. If not given, the last axis is used.
norm{“backward”, “ortho”, “forward”}, optional: Normalization mode. Default is “backward”, meaning no normalization on the forward transforms and scaling by 1/n on the ifft. “forward” instead applies the 1/n factor on the forward tranform. For norm="ortho", both directions are scaled by 1/sqrt(n).

New in version 1.6.0: norm={"forward", "backward"} options were added
overwrite_xbool, optional: If True, the contents of x can be destroyed; the default is False. See the notes below for more details.
workersint, optional: Maximum number of workers to use for parallel computation. If negative, the value wraps around from os.cpu_count(). See below for more details.
planobject, optional: This argument is reserved for passing in a precomputed plan provided by downstream FFT vendors. It is currently not used in SciPy.

New in version 1.5.0.

Returns:

outcomplex ndarray: The truncated or zero-padded input, transformed along the axis indicated by axis, or the last one if axis is not specified.

Raises:

IndexError: if axes is larger than the last axis of x.

See also

ifft: The inverse of fft.
fft2: The 2-D FFT.
fftn: The N-D FFT.
rfftn: The N-D FFT of real input.
fftfreq: Frequency bins for given FFT parameters.
next_fast_len: Size to pad input to for most efficient transforms

Notes

FFT (Fast Fourier Transform) refers to a way the discrete Fourier Transform (DFT) can be calculated efficiently, by using symmetries in the calculated terms. The symmetry is highest when n is a power of 2, and the transform is therefore most efficient for these sizes. For poorly factorizable sizes, scipy.fft uses Bluestein’s algorithm [2] and so is never worse than O(n log n). Further performance improvements may be seen by zero-padding the input using next_fast_len.

If x is a 1d array, then the fft is equivalent to

y[k] = np.sum(x * np.exp(-2j * np.pi * k * np.arange(n)/n))

The frequency term f=k/n is found at y[k]. At y[n/2] we reach the Nyquist frequency and wrap around to the negative-frequency terms. So, for an 8-point transform, the frequencies of the result are [0, 1, 2, 3, -4, -3, -2, -1]. To rearrange the fft output so that the zero-frequency component is centered, like [-4, -3, -2, -1, 0, 1, 2, 3], use fftshift.

Transforms can be done in single, double, or extended precision (long double) floating point. Half precision inputs will be converted to single precision and non-floating-point inputs will be converted to double precision.

If the data type of x is real, a “real FFT” algorithm is automatically used, which roughly halves the computation time. To increase efficiency a little further, use rfft, which does the same calculation, but only outputs half of the symmetrical spectrum. If the data are both real and symmetrical, the dct can again double the efficiency, by generating half of the spectrum from half of the signal.

When overwrite_x=True is specified, the memory referenced by x may be used by the implementation in any way. This may include reusing the memory for the result, but this is in no way guaranteed. You should not rely on the contents of x after the transform as this may change in future without warning.

The workers argument specifies the maximum number of parallel jobs to split the FFT computation into. This will execute independent 1-D FFTs within x. So, x must be at least 2-D and the non-transformed axes must be large enough to split into chunks. If x is too small, fewer jobs may be used than requested.

References

[1]

Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301.

[2]

Bluestein, L., 1970, “A linear filtering approach to the computation of discrete Fourier transform”. IEEE Transactions on Audio and Electroacoustics. 18 (4): 451-455.

Examples

>>> import scipy.fft
>>> import numpy as np
>>> scipy.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

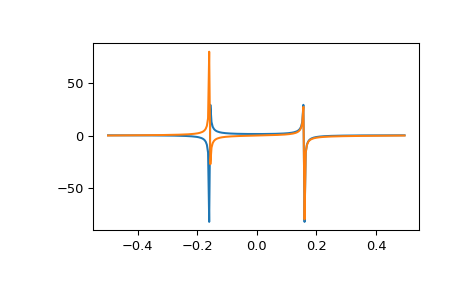
In this example, real input has an FFT which is Hermitian, i.e., symmetric in the real part and anti-symmetric in the imaginary part:

>>> from scipy.fft import fft, fftfreq, fftshift
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = fftshift(fft(np.sin(t)))
>>> freq = fftshift(fftfreq(t.shape[-1]))
>>> plt.plot(freq, sp.real, freq, sp.imag)
[<matplotlib.lines.Line2D object at 0x...>, <matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()