scipy.stats.kstwobign

scipy.stats.kstwobign = <scipy.stats._continuous_distns.kstwobign_gen object>

Limiting distribution of scaled Kolmogorov-Smirnov two-sided test statistic.

This is the asymptotic distribution of the two-sided Kolmogorov-Smirnov statistic \(\sqrt{n} D_n\) that measures the maximum absolute distance of the theoretical (continuous) CDF from the empirical CDF. (see kstest).

As an instance of the rv_continuous class, kstwobign object inherits from it a collection of generic methods (see below for the full list), and completes them with details specific for this particular distribution.

See also

ksone, kstwo, kstest

Notes

\(\sqrt{n} D_n\) is given by

\[D_n = \text{sup}_x |F_n(x) - F(x)|\]

where \(F\) is a continuous CDF and \(F_n\) is an empirical CDF. kstwobign describes the asymptotic distribution (i.e. the limit of \(\sqrt{n} D_n\)) under the null hypothesis of the KS test that the empirical CDF corresponds to i.i.d. random variates with CDF \(F\).

The probability density above is defined in the “standardized” form. To shift and/or scale the distribution use the loc and scale parameters. Specifically, kstwobign.pdf(x, loc, scale) is identically equivalent to kstwobign.pdf(y) / scale with y = (x - loc) / scale. Note that shifting the location of a distribution does not make it a “noncentral” distribution; noncentral generalizations of some distributions are available in separate classes.

References

[1]

Feller, W. “On the Kolmogorov-Smirnov Limit Theorems for Empirical Distributions”, Ann. Math. Statist. Vol 19, 177-189 (1948).

Examples

>>> import numpy as np
>>> from scipy.stats import kstwobign
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

Calculate the first four moments:

>>> mean, var, skew, kurt = kstwobign.stats(moments='mvsk')

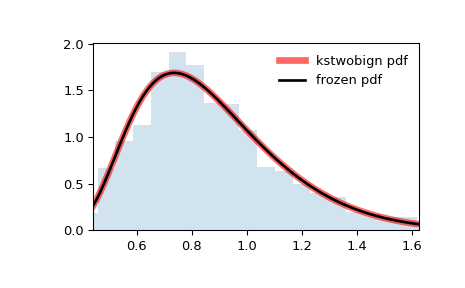
Display the probability density function (pdf):

>>> x = np.linspace(kstwobign.ppf(0.01),
...                 kstwobign.ppf(0.99), 100)
>>> ax.plot(x, kstwobign.pdf(x),
...        'r-', lw=5, alpha=0.6, label='kstwobign pdf')

Alternatively, the distribution object can be called (as a function) to fix the shape, location and scale parameters. This returns a “frozen” RV object holding the given parameters fixed.

Freeze the distribution and display the frozen pdf:

>>> rv = kstwobign()
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

Check accuracy of cdf and ppf:

>>> vals = kstwobign.ppf([0.001, 0.5, 0.999])
>>> np.allclose([0.001, 0.5, 0.999], kstwobign.cdf(vals))
True

Generate random numbers:

>>> r = kstwobign.rvs(size=1000)

And compare the histogram:

>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2)
>>> ax.set_xlim([x[0], x[-1]])
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

Methods

rvs(loc=0, scale=1, size=1, random_state=None)	Random variates.
pdf(x, loc=0, scale=1)	Probability density function.
logpdf(x, loc=0, scale=1)	Log of the probability density function.
cdf(x, loc=0, scale=1)	Cumulative distribution function.
logcdf(x, loc=0, scale=1)	Log of the cumulative distribution function.
sf(x, loc=0, scale=1)	Survival function (also defined as 1 - cdf, but sf is sometimes more accurate).
logsf(x, loc=0, scale=1)	Log of the survival function.
ppf(q, loc=0, scale=1)	Percent point function (inverse of cdf — percentiles).
isf(q, loc=0, scale=1)	Inverse survival function (inverse of sf).
moment(order, loc=0, scale=1)	Non-central moment of the specified order.
stats(loc=0, scale=1, moments=’mv’)	Mean(‘m’), variance(‘v’), skew(‘s’), and/or kurtosis(‘k’).
entropy(loc=0, scale=1)	(Differential) entropy of the RV.
fit(data)	Parameter estimates for generic data. See scipy.stats.rv_continuous.fit for detailed documentation of the keyword arguments.
expect(func, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Expected value of a function (of one argument) with respect to the distribution.
median(loc=0, scale=1)	Median of the distribution.
mean(loc=0, scale=1)	Mean of the distribution.
var(loc=0, scale=1)	Variance of the distribution.
std(loc=0, scale=1)	Standard deviation of the distribution.
interval(confidence, loc=0, scale=1)	Confidence interval with equal areas around the median.