scipy.special.yn_zeros

scipy.special.yn_zeros(n, nt)

Compute zeros of integer-order Bessel function Yn(x).

Compute nt zeros of the functions \(Y_n(x)\) on the interval \((0, \infty)\). The zeros are returned in ascending order.

Parameters:

nint

Order of Bessel function

ntint

Number of zeros to return

Returns:

ndarray

First nt zeros of the Bessel function.

See also

yn

Bessel function of the second kind for integer order

yv

Bessel function of the second kind for real order

References

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Examples

Compute the first four roots of \(Y_2\).

>>> from scipy.special import yn_zeros
>>> yn_zeros(2, 4)
array([ 3.38424177,  6.79380751, 10.02347798, 13.20998671])

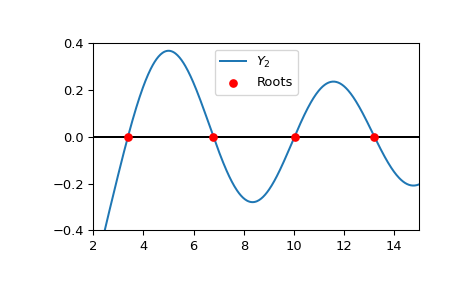
Plot \(Y_2\) and its first four roots.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import yn, yn_zeros
>>> xmin = 2
>>> xmax = 15
>>> x = np.linspace(xmin, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.hlines(0, xmin, xmax, color='k')
>>> ax.plot(x, yn(2, x), label=r'$Y_2$')
>>> ax.scatter(yn_zeros(2, 4), np.zeros((4, )), s=30, c='r',
...            label='Roots', zorder=5)
>>> ax.set_ylim(-0.4, 0.4)
>>> ax.set_xlim(xmin, xmax)
>>> plt.legend()
>>> plt.show()