scipy.special.smirnov

scipy.special.smirnov(n, d, out=None) = <ufunc 'smirnov'>

Kolmogorov-Smirnov complementary cumulative distribution function

Returns the exact Kolmogorov-Smirnov complementary cumulative distribution function,(aka the Survival Function) of Dn+ (or Dn-) for a one-sided test of equality between an empirical and a theoretical distribution. It is equal to the probability that the maximum difference between a theoretical distribution and an empirical one based on n samples is greater than d.

Parameters:

nint

Number of samples

dfloat array_like

Deviation between the Empirical CDF (ECDF) and the target CDF.

outndarray, optional

Optional output array for the function results

Returns:

scalar or ndarray

The value(s) of smirnov(n, d), Prob(Dn+ >= d) (Also Prob(Dn- >= d))

See also

smirnovi

The Inverse Survival Function for the distribution

scipy.stats.ksone

Provides the functionality as a continuous distribution

kolmogorov, kolmogi

Functions for the two-sided distribution

Notes

smirnov is used by stats.kstest in the application of the Kolmogorov-Smirnov Goodness of Fit test. For historial reasons this function is exposed in scpy.special, but the recommended way to achieve the most accurate CDF/SF/PDF/PPF/ISF computations is to use the stats.ksone distribution.

Examples

>>> import numpy as np
>>> from scipy.special import smirnov
>>> from scipy.stats import norm

Show the probability of a gap at least as big as 0, 0.5 and 1.0 for a sample of size 5.

>>> smirnov(5, [0, 0.5, 1.0])
array([ 1.   ,  0.056,  0.   ])

Compare a sample of size 5 against N(0, 1), the standard normal distribution with mean 0 and standard deviation 1.

x is the sample.

>>> x = np.array([-1.392, -0.135, 0.114, 0.190, 1.82])

>>> target = norm(0, 1)
>>> cdfs = target.cdf(x)
>>> cdfs
array([0.0819612 , 0.44630594, 0.5453811 , 0.57534543, 0.9656205 ])

Construct the empirical CDF and the K-S statistics (Dn+, Dn-, Dn).

>>> n = len(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> cols = np.column_stack([x, ecdfs[1:], cdfs, cdfs - ecdfs[:n],
...                        ecdfs[1:] - cdfs])
>>> with np.printoptions(precision=3):
...    print(cols)
[[-1.392  0.2    0.082  0.082  0.118]
 [-0.135  0.4    0.446  0.246 -0.046]
 [ 0.114  0.6    0.545  0.145  0.055]
 [ 0.19   0.8    0.575 -0.025  0.225]
 [ 1.82   1.     0.966  0.166  0.034]]
>>> gaps = cols[:, -2:]
>>> Dnpm = np.max(gaps, axis=0)
>>> print(f'Dn-={Dnpm[0]:f}, Dn+={Dnpm[1]:f}')
Dn-=0.246306, Dn+=0.224655
>>> probs = smirnov(n, Dnpm)
>>> print(f'For a sample of size {n} drawn from N(0, 1):',
...       f' Smirnov n={n}: Prob(Dn- >= {Dnpm[0]:f}) = {probs[0]:.4f}',
...       f' Smirnov n={n}: Prob(Dn+ >= {Dnpm[1]:f}) = {probs[1]:.4f}',
...       sep='\n')
For a sample of size 5 drawn from N(0, 1):
 Smirnov n=5: Prob(Dn- >= 0.246306) = 0.4711
 Smirnov n=5: Prob(Dn+ >= 0.224655) = 0.5245

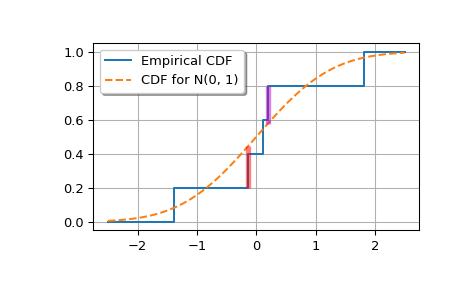
Plot the empirical CDF and the standard normal CDF.

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate(([-2.5], x, [2.5])),
...          np.concatenate((ecdfs, [1])),
...          where='post', label='Empirical CDF')
>>> xx = np.linspace(-2.5, 2.5, 100)
>>> plt.plot(xx, target.cdf(xx), '--', label='CDF for N(0, 1)')

Add vertical lines marking Dn+ and Dn-.

>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus], color='r',
...            alpha=0.5, lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1], color='m',
...            alpha=0.5, lw=4)

>>> plt.grid(True)
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.show()