scipy.special.k0e

scipy.special.k0e(x, out=None) = <ufunc 'k0e'>

Exponentially scaled modified Bessel function K of order 0

Defined as:

k0e(x) = exp(x) * k0(x).

Parameters:

xarray_like

Argument (float)

outndarray, optional

Optional output array for the function values

Returns:

Kscalar or ndarray

Value of the exponentially scaled modified Bessel function K of order 0 at x.

See also

kv

Modified Bessel function of the second kind of any order

k0

Modified Bessel function of the second kind

Notes

The range is partitioned into the two intervals [0, 2] and (2, infinity). Chebyshev polynomial expansions are employed in each interval.

This function is a wrapper for the Cephes [1] routine k0e.

References

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Examples

Calculate the function at one point:

>>> from scipy.special import k0e
>>> k0e(1.)
1.1444630798068947

Calculate the function at several points:

>>> import numpy as np
>>> k0e(np.array([0.5, 2., 3.]))
array([1.52410939, 0.84156822, 0.6977616 ])

Plot the function from 0 to 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0., 10., 1000)
>>> y = k0e(x)
>>> ax.plot(x, y)
>>> plt.show()

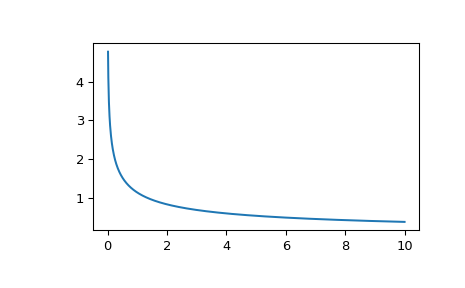
Exponentially scaled Bessel functions are useful for large arguments for which the unscaled Bessel functions are not precise enough.

>>> from scipy.special import k0
>>> k0(1000.)
0.

While k0 returns zero, k0e still returns a finite number:

>>> k0e(1000.)
0.03962832160075422