scipy.special.ive

scipy.special.ive(v, z, out=None) = <ufunc 'ive'>

Exponentially scaled modified Bessel function of the first kind.

Defined as:

ive(v, z) = iv(v, z) * exp(-abs(z.real))

For imaginary numbers without a real part, returns the unscaled Bessel function of the first kind iv.

Parameters:

varray_like of float

Order.

zarray_like of float or complex

Argument.

outndarray, optional

Optional output array for the function values

Returns:

scalar or ndarray

Values of the exponentially scaled modified Bessel function.

See also

iv

Modified Bessel function of the first kind

i0e

Faster implementation of this function for order 0

i1e

Faster implementation of this function for order 1

Notes

For positive v, the AMOS [1] zbesi routine is called. It uses a power series for small z, the asymptotic expansion for large abs(z), the Miller algorithm normalized by the Wronskian and a Neumann series for intermediate magnitudes, and the uniform asymptotic expansions for \(I_v(z)\) and \(J_v(z)\) for large orders. Backward recurrence is used to generate sequences or reduce orders when necessary.

The calculations above are done in the right half plane and continued into the left half plane by the formula,

\[I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\]

(valid when the real part of z is positive). For negative v, the formula

\[I_{-v}(z) = I_v(z) + \frac{2}{\pi} \sin(\pi v) K_v(z)\]

is used, where \(K_v(z)\) is the modified Bessel function of the second kind, evaluated using the AMOS routine zbesk.

References

[1]

Donald E. Amos, “AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order”, http://netlib.org/amos/

Examples

Evaluate the function of order 0 at one point.

>>> import numpy as np
>>> from scipy.special import iv, ive
>>> import matplotlib.pyplot as plt
>>> ive(0, 1.)
0.4657596075936404

Evaluate the function at one point for different orders by providing a list or NumPy array as argument for the v parameter:

>>> ive([0, 1, 1.5], 1.)
array([0.46575961, 0.20791042, 0.10798193])

Evaluate the function at several points for order 0 by providing an array for z.

>>> points = np.array([-2., 0., 3.])
>>> ive(0, points)
array([0.30850832, 1.        , 0.24300035])

Evaluate the function at several points for different orders by providing arrays for both v for z. Both arrays have to be broadcastable to the correct shape. To calculate the orders 0, 1 and 2 for a 1D array of points:

>>> ive([[0], [1], [2]], points)
array([[ 0.30850832,  1.        ,  0.24300035],
       [-0.21526929,  0.        ,  0.19682671],
       [ 0.09323903,  0.        ,  0.11178255]])

Plot the functions of order 0 to 3 from -5 to 5.

>>> fig, ax = plt.subplots()
>>> x = np.linspace(-5., 5., 1000)
>>> for i in range(4):
...     ax.plot(x, ive(i, x), label=f'$I_{i!r}(z)\cdot e^{{-|z|}}$')
>>> ax.legend()
>>> ax.set_xlabel(r"$z$")
>>> plt.show()

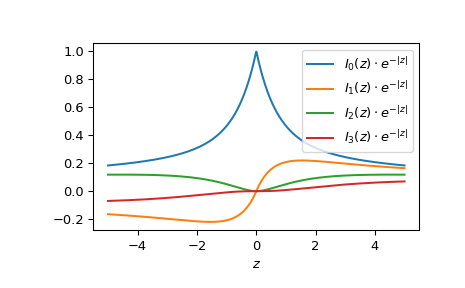
Exponentially scaled Bessel functions are useful for large arguments for which the unscaled Bessel functions over- or underflow. In the following example iv returns infinity whereas ive still returns a finite number.

>>> iv(3, 1000.), ive(3, 1000.)
(inf, 0.01256056218254712)