scipy.special.huber

scipy.special.huber(delta, r, out=None) = <ufunc 'huber'>

Huber loss function.

\[\begin{split}\text{huber}(\delta, r) = \begin{cases} \infty & \delta < 0 \\ \frac{1}{2}r^2 & 0 \le \delta, | r | \le \delta \\ \delta ( |r| - \frac{1}{2}\delta ) & \text{otherwise} \end{cases}\end{split}\]

Parameters:

deltandarray

Input array, indicating the quadratic vs. linear loss changepoint.

rndarray

Input array, possibly representing residuals.

outndarray, optional

Optional output array for the function values

Returns:

scalar or ndarray

The computed Huber loss function values.

See also

pseudo_huber

smooth approximation of this function

Notes

huber is useful as a loss function in robust statistics or machine learning to reduce the influence of outliers as compared to the common squared error loss, residuals with a magnitude higher than delta are not squared [1].

Typically, r represents residuals, the difference between a model prediction and data. Then, for \(|r|\leq\delta\), huber resembles the squared error and for \(|r|>\delta\) the absolute error. This way, the Huber loss often achieves a fast convergence in model fitting for small residuals like the squared error loss function and still reduces the influence of outliers (\(|r|>\delta\)) like the absolute error loss. As \(\delta\) is the cutoff between squared and absolute error regimes, it has to be tuned carefully for each problem. huber is also convex, making it suitable for gradient based optimization.

New in version 0.15.0.

References

[1]

Peter Huber. “Robust Estimation of a Location Parameter”, 1964. Annals of Statistics. 53 (1): 73 - 101.

Examples

Import all necessary modules.

>>> import numpy as np
>>> from scipy.special import huber
>>> import matplotlib.pyplot as plt

Compute the function for delta=1 at r=2

>>> huber(1., 2.)
1.5

Compute the function for different delta by providing a NumPy array or list for delta.

>>> huber([1., 3., 5.], 4.)
array([3.5, 7.5, 8. ])

Compute the function at different points by providing a NumPy array or list for r.

>>> huber(2., np.array([1., 1.5, 3.]))
array([0.5  , 1.125, 4.   ])

The function can be calculated for different delta and r by providing arrays for both with compatible shapes for broadcasting.

>>> r = np.array([1., 2.5, 8., 10.])
>>> deltas = np.array([[1.], [5.], [9.]])
>>> print(r.shape, deltas.shape)
(4,) (3, 1)

>>> huber(deltas, r)
array([[ 0.5  ,  2.   ,  7.5  ,  9.5  ],
       [ 0.5  ,  3.125, 27.5  , 37.5  ],
       [ 0.5  ,  3.125, 32.   , 49.5  ]])

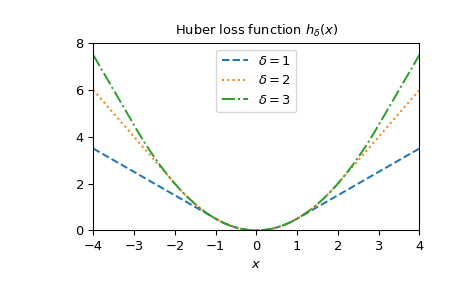
Plot the function for different delta.

>>> x = np.linspace(-4, 4, 500)
>>> deltas = [1, 2, 3]
>>> linestyles = ["dashed", "dotted", "dashdot"]
>>> fig, ax = plt.subplots()
>>> combined_plot_parameters = list(zip(deltas, linestyles))
>>> for delta, style in combined_plot_parameters:
...     ax.plot(x, huber(delta, x), label=f"$\delta={delta}$", ls=style)
>>> ax.legend(loc="upper center")
>>> ax.set_xlabel("$x$")
>>> ax.set_title("Huber loss function $h_{\delta}(x)$")
>>> ax.set_xlim(-4, 4)
>>> ax.set_ylim(0, 8)
>>> plt.show()