scipy.ndimage.gaussian_filter1d

scipy.ndimage.gaussian_filter1d(input, sigma, axis=-1, order=0, output=None, mode='reflect', cval=0.0, truncate=4.0)

One-dimensional Gaussian filter.

Parameters:

input : array_like

The input array.

sigma : scalar

standard deviation for Gaussian kernel

axis : int, optional

The axis of input along which to calculate. Default is -1.

order : int, optional

An order of 0 corresponds to convolution with a Gaussian kernel. A positive order corresponds to convolution with that derivative of a Gaussian.

output : array or dtype, optional

The array in which to place the output, or the dtype of the returned array. By default an array of the same dtype as input will be created.

mode : {‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, optional

The mode parameter determines how the input array is extended when the filter overlaps a border. Default is ‘reflect’. Behavior for each valid value is as follows:

‘reflect’ (d c b a | a b c d | d c b a)

The input is extended by reflecting about the edge of the last pixel.

‘constant’ (k k k k | a b c d | k k k k)

The input is extended by filling all values beyond the edge with the same constant value, defined by the cval parameter.

‘nearest’ (a a a a | a b c d | d d d d)

The input is extended by replicating the last pixel.

‘mirror’ (d c b | a b c d | c b a)

The input is extended by reflecting about the center of the last pixel.

‘wrap’ (a b c d | a b c d | a b c d)

The input is extended by wrapping around to the opposite edge.

cval : scalar, optional

Value to fill past edges of input if mode is ‘constant’. Default is 0.0.

truncate : float, optional

Truncate the filter at this many standard deviations. Default is 4.0.

Returns:

gaussian_filter1d : ndarray

Examples

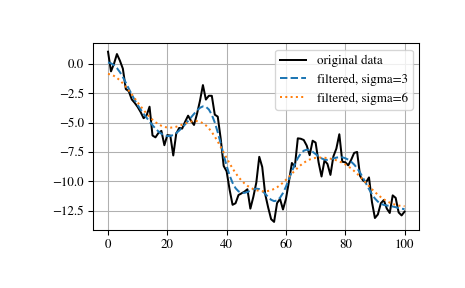
>>> from scipy.ndimage import gaussian_filter1d
>>> gaussian_filter1d([1.0, 2.0, 3.0, 4.0, 5.0], 1)
array([ 1.42704095,  2.06782203,  3.        ,  3.93217797,  4.57295905])
>>> gaussian_filter1d([1.0, 2.0, 3.0, 4.0, 5.0], 4)
array([ 2.91948343,  2.95023502,  3.        ,  3.04976498,  3.08051657])
>>> import matplotlib.pyplot as plt
>>> np.random.seed(280490)
>>> x = np.random.randn(101).cumsum()
>>> y3 = gaussian_filter1d(x, 3)
>>> y6 = gaussian_filter1d(x, 6)
>>> plt.plot(x, 'k', label='original data')
>>> plt.plot(y3, '--', label='filtered, sigma=3')
>>> plt.plot(y6, ':', label='filtered, sigma=6')
>>> plt.legend()
>>> plt.grid()
>>> plt.show()