scipy.integrate.solve_bvp

scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0)

Solve a boundary-value problem for a system of ODEs.

This function numerically solves a first order system of ODEs subject to two-point boundary conditions:

dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b
bc(y(a), y(b), p) = 0

Here x is a 1-dimensional independent variable, y(x) is a n-dimensional vector-valued function and p is a k-dimensional vector of unknown parameters which is to be found along with y(x). For the problem to be determined there must be n + k boundary conditions, i.e. bc must be (n + k)-dimensional function.

The last singular term in the right-hand side of the system is optional. It is defined by an n-by-n matrix S, such that the solution must satisfy S y(a) = 0. This condition will be forced during iterations, so it must not contradict boundary conditions. See [2] for the explanation how this term is handled when solving BVPs numerically.

Problems in a complex domain can be solved as well. In this case y and p are considered to be complex, and f and bc are assumed to be complex-valued functions, but x stays real. Note that f and bc must be complex differentiable (satisfy Cauchy-Riemann equations [4]), otherwise you should rewrite your problem for real and imaginary parts separately. To solve a problem in a complex domain, pass an initial guess for y with a complex data type (see below).

Parameters:

fun : callable

Right-hand side of the system. The calling signature is fun(x, y), or fun(x, y, p) if parameters are present. All arguments are ndarray: x with shape (m,), y with shape (n, m), meaning that y[:, i] corresponds to x[i], and p with shape (k,). The return value must be an array with shape (n, m) and with the same layout as y.

bc : callable

Function evaluating residuals of the boundary conditions. The calling signature is bc(ya, yb), or bc(ya, yb, p) if parameters are present. All arguments are ndarray: ya and yb with shape (n,), and p with shape (k,). The return value must be an array with shape (n + k,).

x : array_like, shape (m,)

Initial mesh. Must be a strictly increasing sequence of real numbers with x[0]=a and x[-1]=b.

y : array_like, shape (n, m)

Initial guess for the function values at the mesh nodes, i-th column corresponds to x[i]. For problems in a complex domain pass y with a complex data type (even if the initial guess is purely real).

p : array_like with shape (k,) or None, optional

Initial guess for the unknown parameters. If None (default), it is assumed that the problem doesn’t depend on any parameters.

S : array_like with shape (n, n) or None

Matrix defining the singular term. If None (default), the problem is solved without the singular term.

fun_jac : callable or None, optional

Function computing derivatives of f with respect to y and p. The calling signature is fun_jac(x, y), or fun_jac(x, y, p) if parameters are present. The return must contain 1 or 2 elements in the following order:

• df_dy : array_like with shape (n, n, m) where an element (i, j, q) equals to d f_i(x_q, y_q, p) / d (y_q)_j.
• df_dp : array_like with shape (n, k, m) where an element (i, j, q) equals to d f_i(x_q, y_q, p) / d p_j.

Here q numbers nodes at which x and y are defined, whereas i and j number vector components. If the problem is solved without unknown parameters df_dp should not be returned.

If fun_jac is None (default), the derivatives will be estimated by the forward finite differences.

bc_jac : callable or None, optional

Function computing derivatives of bc with respect to ya, yb and p. The calling signature is bc_jac(ya, yb), or bc_jac(ya, yb, p) if parameters are present. The return must contain 2 or 3 elements in the following order:

• dbc_dya : array_like with shape (n, n) where an element (i, j) equals to d bc_i(ya, yb, p) / d ya_j.
• dbc_dyb : array_like with shape (n, n) where an element (i, j) equals to d bc_i(ya, yb, p) / d yb_j.
• dbc_dp : array_like with shape (n, k) where an element (i, j) equals to d bc_i(ya, yb, p) / d p_j.

If the problem is solved without unknown parameters dbc_dp should not be returned.

If bc_jac is None (default), the derivatives will be estimated by the forward finite differences.

tol : float, optional

Desired tolerance of the solution. If we define r = y' - f(x, y) where y is the found solution, then the solver tries to achieve on each mesh interval norm(r / (1 + abs(f)) < tol, where norm is estimated in a root mean squared sense (using a numerical quadrature formula). Default is 1e-3.

max_nodes : int, optional

Maximum allowed number of the mesh nodes. If exceeded, the algorithm terminates. Default is 1000.

verbose : {0, 1, 2}, optional

Level of algorithm’s verbosity:

• 0 (default) : work silently.
• 1 : display a termination report.
• 2 : display progress during iterations.

Returns:

Bunch object with the following fields defined:

sol : PPoly

Found solution for y as scipy.interpolate.PPoly instance, a C1 continuous cubic spline.

p : ndarray or None, shape (k,)

Found parameters. None, if the parameters were not present in the problem.

x : ndarray, shape (m,)

Nodes of the final mesh.

y : ndarray, shape (n, m)

Solution values at the mesh nodes.

yp : ndarray, shape (n, m)

Solution derivatives at the mesh nodes.

rms_residuals : ndarray, shape (m - 1,)

RMS values of the relative residuals over each mesh interval (see the description of tol parameter).

niter : int

Number of completed iterations.

status : int

Reason for algorithm termination:

• 0: The algorithm converged to the desired accuracy.
• 1: The maximum number of mesh nodes is exceeded.
• 2: A singular Jacobian encountered when solving the collocation system.

message : string

Verbal description of the termination reason.

success : bool

True if the algorithm converged to the desired accuracy (status=0).

Notes

This function implements a 4-th order collocation algorithm with the control of residuals similar to [1]. A collocation system is solved by a damped Newton method with an affine-invariant criterion function as described in [3].

Note that in [1] integral residuals are defined without normalization by interval lengths. So their definition is different by a multiplier of h**0.5 (h is an interval length) from the definition used here.

New in version 0.18.0.

References

[1]	(1, 2, 3) J. Kierzenka, L. F. Shampine, “A BVP Solver Based on Residual Control and the Maltab PSE”, ACM Trans. Math. Softw., Vol. 27, Number 3, pp. 299-316, 2001.

[2]	(1, 2) L.F. Shampine, P. H. Muir and H. Xu, “A User-Friendly Fortran BVP Solver”.

[3]	(1, 2) U. Ascher, R. Mattheij and R. Russell “Numerical Solution of Boundary Value Problems for Ordinary Differential Equations”.

[4]	(1, 2) Cauchy-Riemann equations on Wikipedia.

Examples

In the first example we solve Bratu’s problem:

y'' + k * exp(y) = 0
y(0) = y(1) = 0

for k = 1.

We rewrite the equation as a first order system and implement its right-hand side evaluation:

y1' = y2
y2' = -exp(y1)

>>> def fun(x, y):
...     return np.vstack((y[1], -np.exp(y[0])))

Implement evaluation of the boundary condition residuals:

>>> def bc(ya, yb):
...     return np.array([ya[0], yb[0]])

Define the initial mesh with 5 nodes:

>>> x = np.linspace(0, 1, 5)

This problem is known to have two solutions. To obtain both of them we use two different initial guesses for y. We denote them by subscripts a and b.

>>> y_a = np.zeros((2, x.size))
>>> y_b = np.zeros((2, x.size))
>>> y_b[0] = 3

Now we are ready to run the solver.

>>> from scipy.integrate import solve_bvp
>>> res_a = solve_bvp(fun, bc, x, y_a)
>>> res_b = solve_bvp(fun, bc, x, y_b)

Let’s plot the two found solutions. We take an advantage of having the solution in a spline form to produce a smooth plot.

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot_a = res_a.sol(x_plot)[0]
>>> y_plot_b = res_b.sol(x_plot)[0]
>>> import matplotlib.pyplot as plt
>>> plt.plot(x_plot, y_plot_a, label='y_a')
>>> plt.plot(x_plot, y_plot_b, label='y_b')
>>> plt.legend()
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()

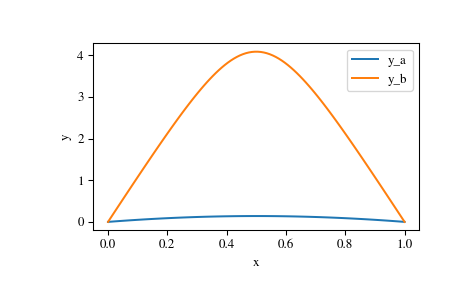
We see that the two solutions have similar shape, but differ in scale significantly.

In the second example we solve a simple Sturm-Liouville problem:

y'' + k**2 * y = 0
y(0) = y(1) = 0

It is known that a non-trivial solution y = A * sin(k * x) is possible for k = pi * n, where n is an integer. To establish the normalization constant A = 1 we add a boundary condition:

y'(0) = k

Again we rewrite our equation as a first order system and implement its right-hand side evaluation:

y1' = y2
y2' = -k**2 * y1

>>> def fun(x, y, p):
...     k = p[0]
...     return np.vstack((y[1], -k**2 * y[0]))

Note that parameters p are passed as a vector (with one element in our case).

Implement the boundary conditions:

>>> def bc(ya, yb, p):
...     k = p[0]
...     return np.array([ya[0], yb[0], ya[1] - k])

Setup the initial mesh and guess for y. We aim to find the solution for k = 2 * pi, to achieve that we set values of y to approximately follow sin(2 * pi * x):

>>> x = np.linspace(0, 1, 5)
>>> y = np.zeros((2, x.size))
>>> y[0, 1] = 1
>>> y[0, 3] = -1

Run the solver with 6 as an initial guess for k.

>>> sol = solve_bvp(fun, bc, x, y, p=[6])

We see that the found k is approximately correct:

>>> sol.p[0]
6.28329460046

And finally plot the solution to see the anticipated sinusoid:

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot = sol.sol(x_plot)[0]
>>> plt.plot(x_plot, y_plot)
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()