scipy.interpolate.CubicSpline

class scipy.interpolate.CubicSpline(x, y, axis=0, bc_type='not-a-knot', extrapolate=None)

Cubic spline data interpolator.

Interpolate data with a piecewise cubic polynomial which is twice continuously differentiable [R85]. The result is represented as a PPoly instance with breakpoints matching the given data.

Parameters:

x : array_like, shape (n,)

1-d array containing values of the independent variable. Values must be real, finite and in strictly increasing order.

y : array_like

Array containing values of the dependent variable. It can have arbitrary number of dimensions, but the length along axis (see below) must match the length of x. Values must be finite.

axis : int, optional

Axis along which y is assumed to be varying. Meaning that for x[i] the corresponding values are np.take(y, i, axis=axis). Default is 0.

bc_type : string or 2-tuple, optional

Boundary condition type. Two additional equations, given by the boundary conditions, are required to determine all coefficients of polynomials on each segment [R86].

If bc_type is a string, then the specified condition will be applied at both ends of a spline. Available conditions are:

• ‘not-a-knot’ (default): The first and second segment at a curve end are the same polynomial. It is a good default when there is no information on boundary conditions.
• ‘periodic’: The interpolated functions is assumed to be periodic of period x[-1] - x[0]. The first and last value of y must be identical: y[0] == y[-1]. This boundary condition will result in y'[0] == y'[-1] and y''[0] == y''[-1].
• ‘clamped’: The first derivative at curves ends are zero. Assuming a 1D y, bc_type=((1, 0.0), (1, 0.0)) is the same condition.
• ‘natural’: The second derivative at curve ends are zero. Assuming a 1D y, bc_type=((2, 0.0), (2, 0.0)) is the same condition.

If bc_type is a 2-tuple, the first and the second value will be applied at the curve start and end respectively. The tuple values can be one of the previously mentioned strings (except ‘periodic’) or a tuple (order, deriv_values) allowing to specify arbitrary derivatives at curve ends:

• order: the derivative order, 1 or 2.
• deriv_value: array_like containing derivative values, shape must be the same as y, excluding axis dimension. For example, if y is 1D, then deriv_value must be a scalar. If y is 3D with the shape (n0, n1, n2) and axis=2, then deriv_value must be 2D and have the shape (n0, n1).

extrapolate : {bool, ‘periodic’, None}, optional

If bool, determines whether to extrapolate to out-of-bounds points based on first and last intervals, or to return NaNs. If ‘periodic’, periodic extrapolation is used. If None (default), extrapolate is set to ‘periodic’ for bc_type='periodic' and to True otherwise.

See also

Akima1DInterpolator, PchipInterpolator, PPoly

Notes

Parameters bc_type and interpolate work independently, i.e. the former controls only construction of a spline, and the latter only evaluation.

When a boundary condition is ‘not-a-knot’ and n = 2, it is replaced by a condition that the first derivative is equal to the linear interpolant slope. When both boundary conditions are ‘not-a-knot’ and n = 3, the solution is sought as a parabola passing through given points.

When ‘not-a-knot’ boundary conditions is applied to both ends, the resulting spline will be the same as returned by splrep (with s=0) and InterpolatedUnivariateSpline, but these two methods use a representation in B-spline basis.

New in version 0.18.0.

References

[R85]

(1, 2) Cubic Spline Interpolation on Wikiversity.

[R86]

(1, 2) Carl de Boor, “A Practical Guide to Splines”, Springer-Verlag, 1978.

Examples

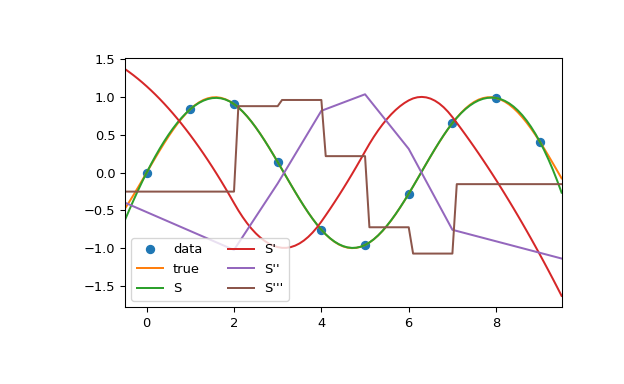
In this example the cubic spline is used to interpolate a sampled sinusoid. You can see that the spline continuity property holds for the first and second derivatives and violates only for the third derivative.

>>> from scipy.interpolate import CubicSpline
>>> import matplotlib.pyplot as plt
>>> x = np.arange(10)
>>> y = np.sin(x)
>>> cs = CubicSpline(x, y)
>>> xs = np.arange(-0.5, 9.6, 0.1)
>>> plt.figure(figsize=(6.5, 4))
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xs, np.sin(xs), label='true')
>>> plt.plot(xs, cs(xs), label="S")
>>> plt.plot(xs, cs(xs, 1), label="S'")
>>> plt.plot(xs, cs(xs, 2), label="S''")
>>> plt.plot(xs, cs(xs, 3), label="S'''")
>>> plt.xlim(-0.5, 9.5)
>>> plt.legend(loc='lower left', ncol=2)
>>> plt.show()

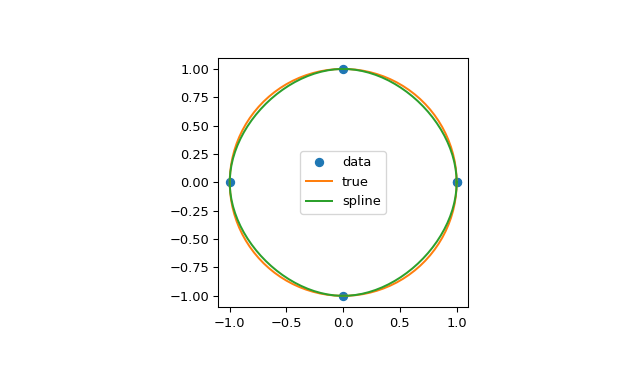
In the second example, the unit circle is interpolated with a spline. A periodic boundary condition is used. You can see that the first derivative values, ds/dx=0, ds/dy=1 at the periodic point (1, 0) are correctly computed. Note that a circle cannot be exactly represented by a cubic spline. To increase precision, more breakpoints would be required.

>>> theta = 2 * np.pi * np.linspace(0, 1, 5)
>>> y = np.c_[np.cos(theta), np.sin(theta)]
>>> cs = CubicSpline(theta, y, bc_type='periodic')
>>> print("ds/dx={:.1f} ds/dy={:.1f}".format(cs(0, 1)[0], cs(0, 1)[1]))
ds/dx=0.0 ds/dy=1.0
>>> xs = 2 * np.pi * np.linspace(0, 1, 100)
>>> plt.figure(figsize=(6.5, 4))
>>> plt.plot(y[:, 0], y[:, 1], 'o', label='data')
>>> plt.plot(np.cos(xs), np.sin(xs), label='true')
>>> plt.plot(cs(xs)[:, 0], cs(xs)[:, 1], label='spline')
>>> plt.axes().set_aspect('equal')
>>> plt.legend(loc='center')
>>> plt.show()

The third example is the interpolation of a polynomial y = x**3 on the interval 0 <= x<= 1. A cubic spline can represent this function exactly. To achieve that we need to specify values and first derivatives at endpoints of the interval. Note that y’ = 3 * x**2 and thus y’(0) = 0 and y’(1) = 3.

>>> cs = CubicSpline([0, 1], [0, 1], bc_type=((1, 0), (1, 3)))
>>> x = np.linspace(0, 1)
>>> np.allclose(x**3, cs(x))
True

Attributes

x	(ndarray, shape (n,)) Breakpoints. The same x which was passed to the constructor.
c	(ndarray, shape (4, n-1, ...)) Coefficients of the polynomials on each segment. The trailing dimensions match the dimensions of y, excluding axis. For example, if y is 1-d, then c[k, i] is a coefficient for (x-x[i])**(3-k) on the segment between x[i] and x[i+1].
axis	(int) Interpolation axis. The same axis which was passed to the constructor.

Methods

__call__(x[, nu, extrapolate])	Evaluate the piecewise polynomial or its derivative.
derivative([nu])	Construct a new piecewise polynomial representing the derivative.
antiderivative([nu])	Construct a new piecewise polynomial representing the antiderivative.
integrate(a, b[, extrapolate])	Compute a definite integral over a piecewise polynomial.
roots([discontinuity, extrapolate])	Find real roots of the the piecewise polynomial.