Linear Algebra¶
When SciPy is built using the optimized ATLAS LAPACK and BLAS libraries, it has very fast linear algebra capabilities. If you dig deep enough, all of the raw lapack and blas libraries are available for your use for even more speed. In this section, some easier-to-use interfaces to these routines are described.
All of these linear algebra routines expect an object that can be converted into a 2-dimensional array. The output of these routines is also a two-dimensional array. There is a matrix class defined in Numpy, which you can initialize with an appropriate Numpy array in order to get objects for which multiplication is matrix-multiplication instead of the default, element-by-element multiplication.
Matrix Class¶
The matrix class is initialized with the SciPy command mat which is just convenient short-hand for matrix. If you are going to be doing a lot of matrix-math, it is convenient to convert arrays into matrices using this command. One advantage of using the mat command is that you can enter two-dimensional matrices using MATLAB-like syntax with commas or spaces separating columns and semicolons separting rows as long as the matrix is placed in a string passed to mat .
Basic routines¶
Finding Inverse¶
The inverse of a matrix  is the matrix
is the matrix
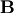 such that
such that 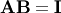 where
where
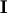 is the identity matrix consisting of ones down the
main diagonal. Usually
is the identity matrix consisting of ones down the
main diagonal. Usually 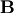 is denoted
is denoted
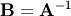 . In SciPy, the matrix inverse of
the Numpy array, A, is obtained using linalg.inv (A) , or
using A.I if A is a Matrix. For example, let
. In SciPy, the matrix inverse of
the Numpy array, A, is obtained using linalg.inv (A) , or
using A.I if A is a Matrix. For example, let
![\[ \mathbf{A=}\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]\]](../_images/math/f15da1511a57d79b59b079b3b1bd20a88c00cbeb.png)
then
![\[ \mathbf{A^{-1}=\frac{1}{25}\left[\begin{array}{ccc} -37 & 9 & 22\\ 14 & 2 & -9\\ 4 & -3 & 1\end{array}\right]=\left[\begin{array}{ccc} -1.48 & 0.36 & 0.88\\ 0.56 & 0.08 & -0.36\\ 0.16 & -0.12 & 0.04\end{array}\right].}\]](../_images/math/6448dc8dd04285fd3eac2290ee7a0d0d5776b5d9.png)
The following example demonstrates this computation in SciPy
>>> A = mat('[1 3 5; 2 5 1; 2 3 8]')
>>> A
matrix([[1, 3, 5],
[2, 5, 1],
[2, 3, 8]])
>>> A.I
matrix([[-1.48, 0.36, 0.88],
[ 0.56, 0.08, -0.36],
[ 0.16, -0.12, 0.04]])
>>> from scipy import linalg
>>> linalg.inv(A)
array([[-1.48, 0.36, 0.88],
[ 0.56, 0.08, -0.36],
[ 0.16, -0.12, 0.04]])
Solving linear system¶
Solving linear systems of equations is straightforward using the scipy command linalg.solve. This command expects an input matrix and a right-hand-side vector. The solution vector is then computed. An option for entering a symmetrix matrix is offered which can speed up the processing when applicable. As an example, suppose it is desired to solve the following simultaneous equations:
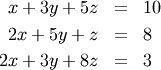
We could find the solution vector using a matrix inverse:
![\[ \left[\begin{array}{c} x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]^{-1}\left[\begin{array}{c} 10\\ 8\\ 3\end{array}\right]=\frac{1}{25}\left[\begin{array}{c} -232\\ 129\\ 19\end{array}\right]=\left[\begin{array}{c} -9.28\\ 5.16\\ 0.76\end{array}\right].\]](../_images/math/10eff05280e41f23e86fae08e79ab0f35ef8e82e.png)
However, it is better to use the linalg.solve command which can be faster and more numerically stable. In this case it however gives the same answer as shown in the following example:
>>> A = mat('[1 3 5; 2 5 1; 2 3 8]')
>>> b = mat('[10;8;3]')
>>> A.I*b
matrix([[-9.28],
[ 5.16],
[ 0.76]])
>>> linalg.solve(A,b)
array([[-9.28],
[ 5.16],
[ 0.76]])
Finding Determinant¶
The determinant of a square matrix  is often denoted
is often denoted
 and is a quantity often used in linear
algebra. Suppose
and is a quantity often used in linear
algebra. Suppose 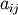 are the elements of the matrix
are the elements of the matrix
 and let
and let 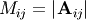 be the determinant of the matrix left by removing the
be the determinant of the matrix left by removing the
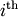 row and
row and 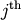 column from
column from
 . Then for any row
. Then for any row 
![\[ \left|\mathbf{A}\right|=\sum_{j}\left(-1\right)^{i+j}a_{ij}M_{ij}.\]](../_images/math/755bef529c1f89f0d1a25bad420ed878c30d985a.png)
This is a recursive way to define the determinant where the base case
is defined by accepting that the determinant of a 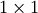 matrix is the only matrix element. In SciPy the determinant can be
calculated with linalg.det . For example, the determinant of
matrix is the only matrix element. In SciPy the determinant can be
calculated with linalg.det . For example, the determinant of
![\[ \mathbf{A=}\left[\begin{array}{ccc} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8\end{array}\right]\]](../_images/math/f15da1511a57d79b59b079b3b1bd20a88c00cbeb.png)
is

In SciPy this is computed as shown in this example:
>>> A = mat('[1 3 5; 2 5 1; 2 3 8]')
>>> linalg.det(A)
-25.000000000000004
Computing norms¶
Matrix and vector norms can also be computed with SciPy. A wide range of norm definitions are available using different parameters to the order argument of linalg.norm . This function takes a rank-1 (vectors) or a rank-2 (matrices) array and an optional order argument (default is 2). Based on these inputs a vector or matrix norm of the requested order is computed.
For vector x , the order parameter can be any real number including inf or -inf. The computed norm is
![\[ \left\Vert \mathbf{x}\right\Vert =\left\{ \begin{array}{cc} \max\left|x_{i}\right| & \textrm{ord}=\textrm{inf}\\ \min\left|x_{i}\right| & \textrm{ord}=-\textrm{inf}\\ \left(\sum_{i}\left|x_{i}\right|^{\textrm{ord}}\right)^{1/\textrm{ord}} & \left|\textrm{ord}\right|<\infty.\end{array}\right.\]](../_images/math/40ce959838b62e756d60da7048ce7b030a6c542b.png)
For matrix  the only valid values for norm are
the only valid values for norm are 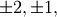
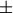 inf, and ‘fro’ (or ‘f’) Thus,
inf, and ‘fro’ (or ‘f’) Thus,
![\[ \left\Vert \mathbf{A}\right\Vert =\left\{ \begin{array}{cc} \max_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=\textrm{inf}\\ \min_{i}\sum_{j}\left|a_{ij}\right| & \textrm{ord}=-\textrm{inf}\\ \max_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=1\\ \min_{j}\sum_{i}\left|a_{ij}\right| & \textrm{ord}=-1\\ \max\sigma_{i} & \textrm{ord}=2\\ \min\sigma_{i} & \textrm{ord}=-2\\ \sqrt{\textrm{trace}\left(\mathbf{A}^{H}\mathbf{A}\right)} & \textrm{ord}=\textrm{'fro'}\end{array}\right.\]](../_images/math/554dc8584731014e0bec0140b3fc7b75c00cde7d.png)
where 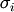 are the singular values of
are the singular values of  .
.
Solving linear least-squares problems and pseudo-inverses¶
Linear least-squares problems occur in many branches of applied
mathematics. In this problem a set of linear scaling coefficients is
sought that allow a model to fit data. In particular it is assumed
that data 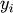 is related to data
is related to data 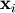 through a set of coefficients
through a set of coefficients 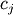 and model functions
and model functions
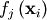 via the model
via the model
![\[ y_{i}=\sum_{j}c_{j}f_{j}\left(\mathbf{x}_{i}\right)+\epsilon_{i}\]](../_images/math/824f8f0c8822fb56f2ebf3820efa3027764c70c3.png)
where 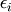 represents uncertainty in the data. The
strategy of least squares is to pick the coefficients
represents uncertainty in the data. The
strategy of least squares is to pick the coefficients 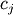 to
minimize
to
minimize
![\[ J\left(\mathbf{c}\right)=\sum_{i}\left|y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right|^{2}.\]](../_images/math/bba7bf382c1b39fb8f7a660d4adc97990b4c83bc.png)
Theoretically, a global minimum will occur when
![\[ \frac{\partial J}{\partial c_{n}^{*}}=0=\sum_{i}\left(y_{i}-\sum_{j}c_{j}f_{j}\left(x_{i}\right)\right)\left(-f_{n}^{*}\left(x_{i}\right)\right)\]](../_images/math/d5e780ba1a0b43644c120d7cdfedf0cd81752b6e.png)
or

where
![\[ \left\{ \mathbf{A}\right\} _{ij}=f_{j}\left(x_{i}\right).\]](../_images/math/f02400ee00eacc33a25c6f7006209fdfef72102b.png)
When 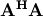 is invertible, then
is invertible, then
![\[ \mathbf{c}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H}\mathbf{y}=\mathbf{A}^{\dagger}\mathbf{y}\]](../_images/math/6dc8365db33468ac649416f9b1ee52fb4d3581fa.png)
where 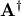 is called the pseudo-inverse of
is called the pseudo-inverse of
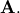 Notice that using this definition of
Notice that using this definition of
 the model can be written
the model can be written
![\[ \mathbf{y}=\mathbf{Ac}+\boldsymbol{\epsilon}.\]](../_images/math/478f15b1c4b3b59f1a1c04a319df7e48d89575dc.png)
The command linalg.lstsq will solve the linear least squares
problem for  given
given  and
and
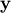 . In addition linalg.pinv or
linalg.pinv2 (uses a different method based on singular value
decomposition) will find
. In addition linalg.pinv or
linalg.pinv2 (uses a different method based on singular value
decomposition) will find 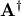 given
given
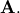
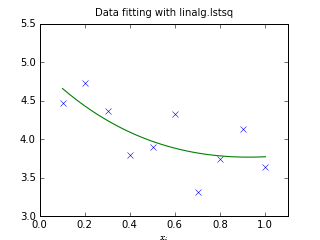
The following example and figure demonstrate the use of linalg.lstsq and linalg.pinv for solving a data-fitting problem. The data shown below were generated using the model:
![\[ y_{i}=c_{1}e^{-x_{i}}+c_{2}x_{i}\]](../_images/math/24ee8d9cd2b039c4556918015d1917b34aa09850.png)
where 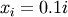 for
for 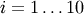 ,
,  ,
and
,
and 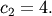 Noise is added to
Noise is added to 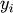 and the
coefficients
and the
coefficients 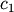 and
and 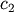 are estimated using
linear least squares.
are estimated using
linear least squares.
>>> from numpy import * >>> from scipy import linalg >>> import matplotlib.pyplot as plt>>> c1,c2= 5.0,2.0 >>> i = r_[1:11] >>> xi = 0.1*i >>> yi = c1*exp(-xi)+c2*xi >>> zi = yi + 0.05*max(yi)*random.randn(len(yi))>>> A = c_[exp(-xi)[:,newaxis],xi[:,newaxis]] >>> c,resid,rank,sigma = linalg.lstsq(A,zi)>>> xi2 = r_[0.1:1.0:100j] >>> yi2 = c[0]*exp(-xi2) + c[1]*xi2>>> plt.plot(xi,zi,'x',xi2,yi2) >>> plt.axis([0,1.1,3.0,5.5]) >>> plt.xlabel('$x_i$') >>> plt.title('Data fitting with linalg.lstsq') >>> plt.show()
(Source code)
Generalized inverse¶
The generalized inverse is calculated using the command
linalg.pinv or linalg.pinv2. These two commands differ
in how they compute the generalized inverse. The first uses the
linalg.lstsq algorithm while the second uses singular value
decomposition. Let  be an
be an 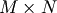 matrix,
then if
matrix,
then if 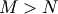 the generalized inverse is
the generalized inverse is
![\[ \mathbf{A}^{\dagger}=\left(\mathbf{A}^{H}\mathbf{A}\right)^{-1}\mathbf{A}^{H}\]](../_images/math/a437038b602ab343b912b2fc73927ca2fc9627f7.png)
while if 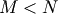 matrix the generalized inverse is
matrix the generalized inverse is
![\[ \mathbf{A}^{\#}=\mathbf{A}^{H}\left(\mathbf{A}\mathbf{A}^{H}\right)^{-1}.\]](../_images/math/f74570d1ea02bded571be7269361aa6de5d7ebad.png)
In both cases for 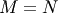 , then
, then
![\[ \mathbf{A}^{\dagger}=\mathbf{A}^{\#}=\mathbf{A}^{-1}\]](../_images/math/a7ccfa366bb288ff51298fd823f6c9bf7e60825b.png)
as long as  is invertible.
is invertible.
Decompositions¶
In many applications it is useful to decompose a matrix using other representations. There are several decompositions supported by SciPy.
Eigenvalues and eigenvectors¶
The eigenvalue-eigenvector problem is one of the most commonly
employed linear algebra operations. In one popular form, the
eigenvalue-eigenvector problem is to find for some square matrix
 scalars
scalars 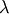 and corresponding vectors
and corresponding vectors
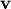 such that
such that
![\[ \mathbf{Av}=\lambda\mathbf{v}.\]](../_images/math/1d8e08b5e0feee938bb177c3f90800f6e2f4a7d4.png)
For an 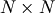 matrix, there are
matrix, there are 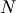 (not necessarily
distinct) eigenvalues — roots of the (characteristic) polynomial
(not necessarily
distinct) eigenvalues — roots of the (characteristic) polynomial
![\[ \left|\mathbf{A}-\lambda\mathbf{I}\right|=0.\]](../_images/math/b2662cca5feccf9301f713f3e7c79a985b641cba.png)
The eigenvectors, 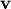 , are also sometimes called right
eigenvectors to distinguish them from another set of left eigenvectors
that satisfy
, are also sometimes called right
eigenvectors to distinguish them from another set of left eigenvectors
that satisfy
![\[ \mathbf{v}_{L}^{H}\mathbf{A}=\lambda\mathbf{v}_{L}^{H}\]](../_images/math/af5d720a35d3b6a2c1ded629d90239b1e25eb9eb.png)
or
![\[ \mathbf{A}^{H}\mathbf{v}_{L}=\lambda^{*}\mathbf{v}_{L}.\]](../_images/math/8774c026418e4bcc15c0fd54ffc01a6303fb3de7.png)
With it’s default optional arguments, the command linalg.eig
returns 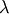 and
and 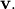 However, it can also
return
However, it can also
return 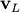 and just
and just 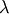 by itself (
linalg.eigvals returns just
by itself (
linalg.eigvals returns just 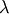 as well).
as well).
In addtion, linalg.eig can also solve the more general eigenvalue problem
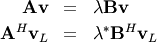
for square matrices  and
and  The
standard eigenvalue problem is an example of the general eigenvalue
problem for
The
standard eigenvalue problem is an example of the general eigenvalue
problem for 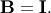 When a generalized
eigenvalue problem can be solved, then it provides a decomposition of
When a generalized
eigenvalue problem can be solved, then it provides a decomposition of
 as
as
![\[ \mathbf{A}=\mathbf{BV}\boldsymbol{\Lambda}\mathbf{V}^{-1}\]](../_images/math/87276d434b87f1d7912ebdd7c3fc7eafacad3ab6.png)
where  is the collection of eigenvectors into
columns and
is the collection of eigenvectors into
columns and 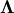 is a diagonal matrix of
eigenvalues.
is a diagonal matrix of
eigenvalues.
By definition, eigenvectors are only defined up to a constant scale
factor. In SciPy, the scaling factor for the eigenvectors is chosen so
that 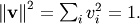
As an example, consider finding the eigenvalues and eigenvectors of the matrix
![\[ \mathbf{A}=\left[\begin{array}{ccc} 1 & 5 & 2\\ 2 & 4 & 1\\ 3 & 6 & 2\end{array}\right].\]](../_images/math/58c752af8057ccb75f3eb73fcf74e012cb8fbbe9.png)
The characteristic polynomial is
![\begin{eqnarray*} \left|\mathbf{A}-\lambda\mathbf{I}\right| & = & \left(1-\lambda\right)\left[\left(4-\lambda\right)\left(2-\lambda\right)-6\right]-\\ & & 5\left[2\left(2-\lambda\right)-3\right]+2\left[12-3\left(4-\lambda\right)\right]\\ & = & -\lambda^{3}+7\lambda^{2}+8\lambda-3.\end{eqnarray*}](../_images/math/67dfe1c28738109b8806fb5d40834ea83eba5352.png)
The roots of this polynomial are the eigenvalues of  :
:
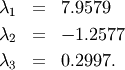
The eigenvectors corresponding to each eigenvalue can be found using the original equation. The eigenvectors associated with these eigenvalues can then be found.
>>> from scipy import linalg >>> A = mat('[1 5 2; 2 4 1; 3 6 2]') >>> la,v = linalg.eig(A) >>> l1,l2,l3 = la >>> print l1, l2, l3 (7.95791620491+0j) (-1.25766470568+0j) (0.299748500767+0j)>>> print v[:,0] [-0.5297175 -0.44941741 -0.71932146] >>> print v[:,1] [-0.90730751 0.28662547 0.30763439] >>> print v[:,2] [ 0.28380519 -0.39012063 0.87593408] >>> print sum(abs(v**2),axis=0) [ 1. 1. 1.]>>> v1 = mat(v[:,0]).T >>> print max(ravel(abs(A*v1-l1*v1))) 8.881784197e-16
Singular value decomposition¶
Singular Value Decompostion (SVD) can be thought of as an extension of
the eigenvalue problem to matrices that are not square. Let
 be an
be an 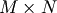 matrix with
matrix with 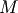 and
and
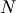 arbitrary. The matrices
arbitrary. The matrices  and
and
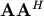 are square hermitian matrices [1] of
size
are square hermitian matrices [1] of
size 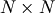 and
and 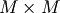 respectively. It is known
that the eigenvalues of square hermitian matrices are real and
non-negative. In addtion, there are at most
respectively. It is known
that the eigenvalues of square hermitian matrices are real and
non-negative. In addtion, there are at most
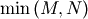 identical non-zero eigenvalues of
identical non-zero eigenvalues of
 and
and 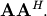 Define these positive eigenvalues as
Define these positive eigenvalues as 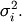 The
square-root of these are called singular values of
The
square-root of these are called singular values of 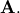 The eigenvectors of
The eigenvectors of  are collected by
columns into an
are collected by
columns into an 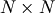 unitary [2] matrix
unitary [2] matrix
 while the eigenvectors of
while the eigenvectors of
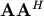 are collected by columns in the
unitary matrix
are collected by columns in the
unitary matrix 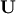 , the singular values are collected
in an
, the singular values are collected
in an 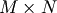 zero matrix
zero matrix
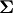 with main diagonal entries set to
the singular values. Then
with main diagonal entries set to
the singular values. Then
![\[ \mathbf{A=U}\boldsymbol{\Sigma}\mathbf{V}^{H}\]](../_images/math/982143dc39add5009746663baf582d6dc728eafa.png)
is the singular-value decomposition of 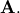 Every
matrix has a singular value decomposition. Sometimes, the singular
values are called the spectrum of
Every
matrix has a singular value decomposition. Sometimes, the singular
values are called the spectrum of 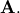 The command
linalg.svd will return
The command
linalg.svd will return 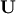 ,
,
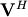 , and
, and 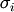 as an array of the
singular values. To obtain the matrix
as an array of the
singular values. To obtain the matrix 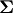 use
linalg.diagsvd. The following example illustrates the use of
linalg.svd .
use
linalg.diagsvd. The following example illustrates the use of
linalg.svd .
>>> A = mat('[1 3 2; 1 2 3]') >>> M,N = A.shape >>> U,s,Vh = linalg.svd(A) >>> Sig = mat(linalg.diagsvd(s,M,N)) >>> U, Vh = mat(U), mat(Vh) >>> print U [[-0.70710678 -0.70710678] [-0.70710678 0.70710678]] >>> print Sig [[ 5.19615242 0. 0. ] [ 0. 1. 0. ]] >>> print Vh [[ -2.72165527e-01 -6.80413817e-01 -6.80413817e-01] [ -6.18652536e-16 -7.07106781e-01 7.07106781e-01] [ -9.62250449e-01 1.92450090e-01 1.92450090e-01]]>>> print A [[1 3 2] [1 2 3]] >>> print U*Sig*Vh [[ 1. 3. 2.] [ 1. 2. 3.]]
| [1] | A hermitian matrix 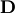 satisfies satisfies 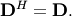 |
| [2] | A unitary matrix 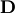 satisfies satisfies 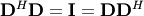 so that so that  |
LU decomposition¶
The LU decompostion finds a representation for the 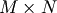 matrix
matrix  as
as
![\[ \mathbf{A}=\mathbf{PLU}\]](../_images/math/6418ca9f0987baa21818b0df8685344a761b56b1.png)
where 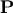 is an
is an 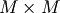 permutation matrix (a
permutation of the rows of the identity matrix),
permutation matrix (a
permutation of the rows of the identity matrix), 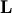 is
in
is
in  lower triangular or trapezoidal matrix (
lower triangular or trapezoidal matrix (
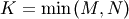 ) with unit-diagonal, and
) with unit-diagonal, and
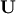 is an upper triangular or trapezoidal matrix. The
SciPy command for this decomposition is linalg.lu .
is an upper triangular or trapezoidal matrix. The
SciPy command for this decomposition is linalg.lu .
Such a decomposition is often useful for solving many simultaneous equations where the left-hand-side does not change but the right hand side does. For example, suppose we are going to solve
![\[ \mathbf{A}\mathbf{x}_{i}=\mathbf{b}_{i}\]](../_images/math/b78d42ead48f836bd05e94dc414deb7186182dfb.png)
for many different 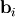 . The LU decomposition allows this to be written as
. The LU decomposition allows this to be written as
![\[ \mathbf{PLUx}_{i}=\mathbf{b}_{i}.\]](../_images/math/19939ea9f3ce9b41602abdd5c749a5aaaacf6905.png)
Because 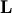 is lower-triangular, the equation can be
solved for
is lower-triangular, the equation can be
solved for 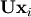 and finally
and finally
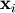 very rapidly using forward- and
back-substitution. An initial time spent factoring
very rapidly using forward- and
back-substitution. An initial time spent factoring  allows for very rapid solution of similar systems of equations in the
future. If the intent for performing LU decomposition is for solving
linear systems then the command linalg.lu_factor should be used
followed by repeated applications of the command
linalg.lu_solve to solve the system for each new
right-hand-side.
allows for very rapid solution of similar systems of equations in the
future. If the intent for performing LU decomposition is for solving
linear systems then the command linalg.lu_factor should be used
followed by repeated applications of the command
linalg.lu_solve to solve the system for each new
right-hand-side.
Cholesky decomposition¶
Cholesky decomposition is a special case of LU decomposition
applicable to Hermitian positive definite matrices. When
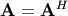 and
and
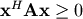 for all
for all 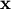 ,
then decompositions of
,
then decompositions of  can be found so that
can be found so that
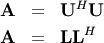
where 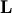 is lower-triangular and
is lower-triangular and 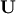 is
upper triangular. Notice that
is
upper triangular. Notice that 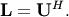 The
command linagl.cholesky computes the cholesky
factorization. For using cholesky factorization to solve systems of
equations there are also linalg.cho_factor and
linalg.cho_solve routines that work similarly to their LU
decomposition counterparts.
The
command linagl.cholesky computes the cholesky
factorization. For using cholesky factorization to solve systems of
equations there are also linalg.cho_factor and
linalg.cho_solve routines that work similarly to their LU
decomposition counterparts.
QR decomposition¶
The QR decomposition (sometimes called a polar decomposition) works
for any 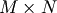 array and finds an
array and finds an 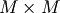 unitary
matrix
unitary
matrix  and an
and an 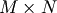 upper-trapezoidal
matrix
upper-trapezoidal
matrix 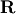 such that
such that
![\[ \mathbf{A=QR}.\]](../_images/math/0110430c3f72562038677ae460f41df5b6edd41f.png)
Notice that if the SVD of  is known then the QR decomposition can be found
is known then the QR decomposition can be found
![\[ \mathbf{A}=\mathbf{U}\boldsymbol{\Sigma}\mathbf{V}^{H}=\mathbf{QR}\]](../_images/math/a0e7336badff32ddb382f78f36a93bbae63e3784.png)
implies that 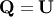 and
and
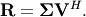 Note, however,
that in SciPy independent algorithms are used to find QR and SVD
decompositions. The command for QR decomposition is linalg.qr .
Note, however,
that in SciPy independent algorithms are used to find QR and SVD
decompositions. The command for QR decomposition is linalg.qr .
Schur decomposition¶
For a square 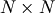 matrix,
matrix,  , the Schur
decomposition finds (not-necessarily unique) matrices
, the Schur
decomposition finds (not-necessarily unique) matrices
 and
and 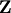 such that
such that
![\[ \mathbf{A}=\mathbf{ZT}\mathbf{Z}^{H}\]](../_images/math/63a0676ccac3bd1598fb204e8b85d91d6bc55e50.png)
where 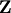 is a unitary matrix and
is a unitary matrix and  is
either upper-triangular or quasi-upper triangular depending on whether
or not a real schur form or complex schur form is requested. For a
real schur form both
is
either upper-triangular or quasi-upper triangular depending on whether
or not a real schur form or complex schur form is requested. For a
real schur form both  and
and 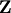 are
real-valued when
are
real-valued when  is real-valued. When
is real-valued. When
 is a real-valued matrix the real schur form is only
quasi-upper triangular because
is a real-valued matrix the real schur form is only
quasi-upper triangular because  blocks extrude from
the main diagonal corresponding to any complex- valued
eigenvalues. The command linalg.schur finds the Schur
decomposition while the command linalg.rsf2csf converts
blocks extrude from
the main diagonal corresponding to any complex- valued
eigenvalues. The command linalg.schur finds the Schur
decomposition while the command linalg.rsf2csf converts
 and
and 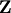 from a real Schur form to a
complex Schur form. The Schur form is especially useful in calculating
functions of matrices.
from a real Schur form to a
complex Schur form. The Schur form is especially useful in calculating
functions of matrices.
The following example illustrates the schur decomposition:
>>> from scipy import linalg
>>> A = mat('[1 3 2; 1 4 5; 2 3 6]')
>>> T,Z = linalg.schur(A)
>>> T1,Z1 = linalg.schur(A,'complex')
>>> T2,Z2 = linalg.rsf2csf(T,Z)
>>> print T
[[ 9.90012467 1.78947961 -0.65498528]
[ 0. 0.54993766 -1.57754789]
[ 0. 0.51260928 0.54993766]]
>>> print T2
[[ 9.90012467 +0.00000000e+00j -0.32436598 +1.55463542e+00j
-0.88619748 +5.69027615e-01j]
[ 0.00000000 +0.00000000e+00j 0.54993766 +8.99258408e-01j
1.06493862 +1.37016050e-17j]
[ 0.00000000 +0.00000000e+00j 0.00000000 +0.00000000e+00j
0.54993766 -8.99258408e-01j]]
>>> print abs(T1-T2) # different
[[ 1.24357637e-14 2.09205364e+00 6.56028192e-01]
[ 0.00000000e+00 4.00296604e-16 1.83223097e+00]
[ 0.00000000e+00 0.00000000e+00 4.57756680e-16]]
>>> print abs(Z1-Z2) # different
[[ 0.06833781 1.10591375 0.23662249]
[ 0.11857169 0.5585604 0.29617525]
[ 0.12624999 0.75656818 0.22975038]]
>>> T,Z,T1,Z1,T2,Z2 = map(mat,(T,Z,T1,Z1,T2,Z2))
>>> print abs(A-Z*T*Z.H) # same
[[ 1.11022302e-16 4.44089210e-16 4.44089210e-16]
[ 4.44089210e-16 1.33226763e-15 8.88178420e-16]
[ 8.88178420e-16 4.44089210e-16 2.66453526e-15]]
>>> print abs(A-Z1*T1*Z1.H) # same
[[ 1.00043248e-15 2.22301403e-15 5.55749485e-15]
[ 2.88899660e-15 8.44927041e-15 9.77322008e-15]
[ 3.11291538e-15 1.15463228e-14 1.15464861e-14]]
>>> print abs(A-Z2*T2*Z2.H) # same
[[ 3.34058710e-16 8.88611201e-16 4.18773089e-18]
[ 1.48694940e-16 8.95109973e-16 8.92966151e-16]
[ 1.33228956e-15 1.33582317e-15 3.55373104e-15]]
Matrix Functions¶
Consider the function 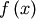 with Taylor series expansion
with Taylor series expansion
![\[ f\left(x\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}x^{k}.\]](../_images/math/adf875f7968f2eacd843a6781a311c30a294d242.png)
A matrix function can be defined using this Taylor series for the
square matrix  as
as
![\[ f\left(\mathbf{A}\right)=\sum_{k=0}^{\infty}\frac{f^{\left(k\right)}\left(0\right)}{k!}\mathbf{A}^{k}.\]](../_images/math/3bb288756a77e30defb3856c78f3f3275944b69d.png)
While, this serves as a useful representation of a matrix function, it is rarely the best way to calculate a matrix function.
Exponential and logarithm functions¶
The matrix exponential is one of the more common matrix functions. It can be defined for square matrices as
![\[ e^{\mathbf{A}}=\sum_{k=0}^{\infty}\frac{1}{k!}\mathbf{A}^{k}.\]](../_images/math/b90c25a79b0bf9a43a7bb678f6285cdf34c63d0f.png)
The command linalg.expm3 uses this Taylor series definition to compute the matrix exponential. Due to poor convergence properties it is not often used.
Another method to compute the matrix exponential is to find an
eigenvalue decomposition of  :
:
![\[ \mathbf{A}=\mathbf{V}\boldsymbol{\Lambda}\mathbf{V}^{-1}\]](../_images/math/7df93fd626a347846d758355a0a222db1375ee2f.png)
and note that
![\[ e^{\mathbf{A}}=\mathbf{V}e^{\boldsymbol{\Lambda}}\mathbf{V}^{-1}\]](../_images/math/913ee63a8b6d027192a8e0eda61fe6a9cb57c67e.png)
where the matrix exponential of the diagonal matrix 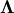 is just the exponential of its elements. This method is implemented in linalg.expm2 .
is just the exponential of its elements. This method is implemented in linalg.expm2 .
The preferred method for implementing the matrix exponential is to use
scaling and a Padé approximation for 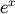 . This algorithm is
implemented as linalg.expm .
. This algorithm is
implemented as linalg.expm .
The inverse of the matrix exponential is the matrix logarithm defined as the inverse of the matrix exponential.
![\[ \mathbf{A}\equiv\exp\left(\log\left(\mathbf{A}\right)\right).\]](../_images/math/32d11c8dcf8b96fa4f2466a53892f850bc713b15.png)
The matrix logarithm can be obtained with linalg.logm .
Trigonometric functions¶
The trigonometric functions 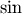 ,
,  , and
, and
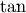 are implemented for matrices in linalg.sinm,
linalg.cosm, and linalg.tanm respectively. The matrix
sin and cosine can be defined using Euler’s identity as
are implemented for matrices in linalg.sinm,
linalg.cosm, and linalg.tanm respectively. The matrix
sin and cosine can be defined using Euler’s identity as
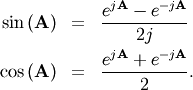
The tangent is
![\[ \tan\left(x\right)=\frac{\sin\left(x\right)}{\cos\left(x\right)}=\left[\cos\left(x\right)\right]^{-1}\sin\left(x\right)\]](../_images/math/430f207b46e2788e19b9cf23f857ab4ac492fe03.png)
and so the matrix tangent is defined as
![\[ \left[\cos\left(\mathbf{A}\right)\right]^{-1}\sin\left(\mathbf{A}\right).\]](../_images/math/3685ed6e1ac7e3a98ea0076b48815f39923f0fe8.png)
Hyperbolic trigonometric functions¶
The hyperbolic trigonemetric functions  ,
,  ,
and
,
and 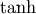 can also be defined for matrices using the familiar
definitions:
can also be defined for matrices using the familiar
definitions:
![\begin{eqnarray*} \sinh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}-e^{-\mathbf{A}}}{2}\\ \cosh\left(\mathbf{A}\right) & = & \frac{e^{\mathbf{A}}+e^{-\mathbf{A}}}{2}\\ \tanh\left(\mathbf{A}\right) & = & \left[\cosh\left(\mathbf{A}\right)\right]^{-1}\sinh\left(\mathbf{A}\right).\end{eqnarray*}](../_images/math/9b414596e47b8daf591e465f76a8bca9bfc3ec26.png)
These matrix functions can be found using linalg.sinhm, linalg.coshm , and linalg.tanhm.
Arbitrary function¶
Finally, any arbitrary function that takes one complex number and returns a complex number can be called as a matrix function using the command linalg.funm. This command takes the matrix and an arbitrary Python function. It then implements an algorithm from Golub and Van Loan’s book “Matrix Computations “to compute function applied to the matrix using a Schur decomposition. Note that the function needs to accept complex numbers as input in order to work with this algorithm. For example the following code computes the zeroth-order Bessel function applied to a matrix.
>>> from scipy import special, random, linalg
>>> A = random.rand(3,3)
>>> B = linalg.funm(A,lambda x: special.jv(0,x))
>>> print A
[[ 0.72578091 0.34105276 0.79570345]
[ 0.65767207 0.73855618 0.541453 ]
[ 0.78397086 0.68043507 0.4837898 ]]
>>> print B
[[ 0.72599893 -0.20545711 -0.22721101]
[-0.27426769 0.77255139 -0.23422637]
[-0.27612103 -0.21754832 0.7556849 ]]
>>> print linalg.eigvals(A)
[ 1.91262611+0.j 0.21846476+0.j -0.18296399+0.j]
>>> print special.jv(0, linalg.eigvals(A))
[ 0.27448286+0.j 0.98810383+0.j 0.99164854+0.j]
>>> print linalg.eigvals(B)
[ 0.27448286+0.j 0.98810383+0.j 0.99164854+0.j]
Note how, by virtue of how matrix analytic functions are defined, the Bessel function has acted on the matrix eigenvalues.