scipy.interpolate.make_interp_spline¶
- scipy.interpolate.make_interp_spline(x, y, k=3, t=None, bc_type=None, axis=0, check_finite=True)[source]¶
Compute the (coefficients of) interpolating B-spline.
Parameters: x : array_like, shape (n,)
Abscissas.
y : array_like, shape (n, ...)
Ordinates.
k : int, optional
B-spline degree. Default is cubic, k=3.
t : array_like, shape (nt + k + 1,), optional.
Knots. The number of knots needs to agree with the number of datapoints and the number of derivatives at the edges. Specifically, nt - n must equal len(deriv_l) + len(deriv_r).
bc_type : 2-tuple or None
Boundary conditions. Default is None, which means choosing the boundary conditions automatically. Otherwise, it must be a length-two tuple where the first element sets the boundary conditions at x[0] and the second element sets the boundary conditions at x[-1]. Each of these must be an iterable of pairs (order, value) which gives the values of derivatives of specified orders at the given edge of the interpolation interval.
axis : int, optional
Interpolation axis. Default is 0.
check_finite : bool, optional
Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs. Default is True.
Returns: b : a BSpline object of the degree k and with knots t.
See also
- BSpline
- base class representing the B-spline objects
- CubicSpline
- a cubic spline in the polynomial basis
- make_lsq_spline
- a similar factory function for spline fitting
- UnivariateSpline
- a wrapper over FITPACK spline fitting routines
- splrep
- a wrapper over FITPACK spline fitting routines
Examples
Use cubic interpolation on Chebyshev nodes:
>>> def cheb_nodes(N): ... jj = 2.*np.arange(N) + 1 ... x = np.cos(np.pi * jj / 2 / N)[::-1] ... return x
>>> x = cheb_nodes(20) >>> y = np.sqrt(1 - x**2)
>>> from scipy.interpolate import BSpline, make_interp_spline >>> b = make_interp_spline(x, y) >>> np.allclose(b(x), y) True
Note that the default is a cubic spline with a not-a-knot boundary condition
>>> b.k 3
Here we use a ‘natural’ spline, with zero 2nd derivatives at edges:
>>> l, r = [(2, 0)], [(2, 0)] >>> b_n = make_interp_spline(x, y, bc_type=(l, r)) >>> np.allclose(b_n(x), y) True >>> x0, x1 = x[0], x[-1] >>> np.allclose([b_n(x0, 2), b_n(x1, 2)], [0, 0]) True
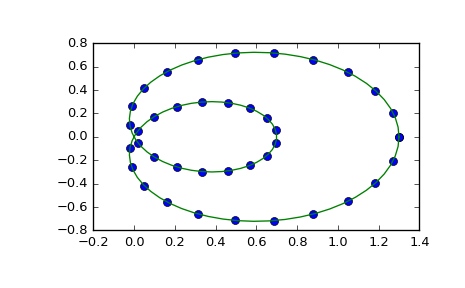
Interpolation of parametric curves is also supported. As an example, we compute a discretization of a snail curve in polar coordinates
>>> phi = np.linspace(0, 2.*np.pi, 40) >>> r = 0.3 + np.cos(phi) >>> x, y = r*np.cos(phi), r*np.sin(phi) # convert to Cartesian coordinates
Build an interpolating curve, parameterizing it by the angle
>>> from scipy.interpolate import make_interp_spline >>> spl = make_interp_spline(phi, np.c_[x, y])
Evaluate the interpolant on a finer grid (note that we transpose the result to unpack it into a pair of x- and y-arrays)
>>> phi_new = np.linspace(0, 2.*np.pi, 100) >>> x_new, y_new = spl(phi_new).T
Plot the result
>>> import matplotlib.pyplot as plt >>> plt.plot(x, y, 'o') >>> plt.plot(x_new, y_new, '-') >>> plt.show()