scipy.interpolate.BSpline

class scipy.interpolate.BSpline(t, c, k, extrapolate=True, axis=0)

Univariate spline in the B-spline basis.

\[S(x) = \sum_{j=0}^{n-1} c_j B_{j, k; t}(x)\]

where \(B_{j, k; t}\) are B-spline basis functions of degree k and knots t.

Parameters:

t : ndarray, shape (n+k+1,)

knots

c : ndarray, shape (>=n, ...)

spline coefficients

k : int

B-spline order

extrapolate : bool, optional

whether to extrapolate beyond the base interval, t[k] .. t[n], or to return nans. If True, extrapolates the first and last polynomial pieces of b-spline functions active on the base interval. Default is True.

axis : int, optional

Interpolation axis. Default is zero.

Notes

B-spline basis elements are defined via

\[\begin{split}B_{i, 0}(x) = 1, \textrm{if $t_i \le x < t_{i+1}$, otherwise $0$,}\end{split}\]\[B_{i, k}(x) = \frac{x - t_i}{t_{i+k} - t_i} B_{i, k-1}(x) + \frac{t_{i+k+1} - x}{t_{i+k+1} - t_{i+1}} B_{i+1, k-1}(x)\]

Implementation details

• At least k+1 coefficients are required for a spline of degree k, so that n >= k+1. Additional coefficients, c[j] with j > n, are ignored.
• B-spline basis elements of degree k form a partition of unity on the base interval, t[k] <= x <= t[n].

References

[R55]

Tom Lyche and Knut Morken, Spline methods, http://www.uio.no/studier/emner/matnat/ifi/INF-MAT5340/v05/undervisningsmateriale/

[R56]

Carl de Boor, A practical guide to splines, Springer, 2001.

Examples

Translating the recursive definition of B-splines into Python code, we have:

>>> def B(x, k, i, t):
...    if k == 0:
...       return 1.0 if t[i] <= x < t[i+1] else 0.0
...    if t[i+k] == t[i]:
...       c1 = 0.0
...    else:
...       c1 = (x - t[i])/(t[i+k] - t[i]) * B(x, k-1, i, t)
...    if t[i+k+1] == t[i+1]:
...       c2 = 0.0
...    else:
...       c2 = (t[i+k+1] - x)/(t[i+k+1] - t[i+1]) * B(x, k-1, i+1, t)
...    return c1 + c2

>>> def bspline(x, t, c, k):
...    n = len(t) - k - 1
...    assert (n >= k+1) and (len(c) >= n)
...    return sum(c[i] * B(x, k, i, t) for i in range(n))

Note that this is an inefficient (if straightforward) way to evaluate B-splines — this spline class does it in an equivalent, but much more efficient way.

Here we construct a quadratic spline function on the base interval 2 <= x <= 4 and compare with the naive way of evaluating the spline:

>>> from scipy.interpolate import BSpline
>>> k = 2
>>> t = [0, 1, 2, 3, 4, 5, 6]
>>> c = [-1, 2, 0, -1]
>>> spl = BSpline(t, c, k)
>>> spl(2.5)
array(1.375)
>>> bspline(2.5, t, c, k)
1.375

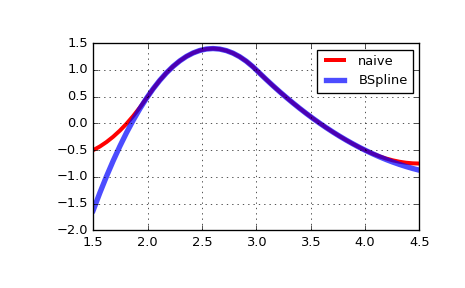
Note that outside of the base interval results differ. This is because BSpline extrapolates the first and last polynomial pieces of b-spline functions active on the base interval.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> xx = np.linspace(1.5, 4.5, 50)
>>> ax.plot(xx, [bspline(x, t, c ,k) for x in xx], 'r-', lw=3, label='naive')
>>> ax.plot(xx, spl(xx), 'b-', lw=4, alpha=0.7, label='BSpline')
>>> ax.grid(True)
>>> ax.legend(loc='best')
>>> plt.show()

(Source code)

Attributes

tck	Equvalent to (self.t, self.c, self.k) (read-only).

t	(ndarray) knot vector
c	(ndarray) spline coefficients
k	(int) spline degree
extrapolate	(bool) If True, extrapolates the first and last polynomial pieces of b-spline functions active on the base interval.
axis	(int) Interpolation axis.

Methods

__call__(x[, nu, extrapolate])	Evaluate a spline function.
basis_element(t[, extrapolate])	Return a B-spline basis element B(x | t[0], ..., t[k+1]).
derivative([nu])	Return a b-spline representing the derivative.
antiderivative([nu])	Return a b-spline representing the antiderivative.
integrate(a, b[, extrapolate])	Compute a definite integral of the spline.
construct_fast(t, c, k[, extrapolate, axis])	Construct a spline without making checks.