scipy.signal.spectrogram

scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=256, noverlap=None, nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1)

Compute a spectrogram with consecutive Fourier transforms.

Spectrograms can be used as a way of visualizing the change of a nonstationary signal’s frequency content over time.

Parameters:

x : array_like

Time series of measurement values

fs : float, optional

Sampling frequency of the x time series. Defaults to 1.0.

window : str or tuple or array_like, optional

Desired window to use. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length will be used for nperseg. Defaults to a Tukey window with shape parameter of 0.25.

nperseg : int, optional

Length of each segment. Defaults to 256.

noverlap : int, optional

Number of points to overlap between segments. If None, noverlap = nperseg // 8. Defaults to None.

nfft : int, optional

Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.

detrend : str or function or False, optional

Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to detrend. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to ‘constant’.

return_onesided : bool, optional

If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Note that for complex data, a two-sided spectrum is always returned.

scaling : { ‘density’, ‘spectrum’ }, optional

Selects between computing the power spectral density (‘density’) where Pxx has units of V**2/Hz and computing the power spectrum (‘spectrum’) where Pxx has units of V**2, if x is measured in V and fs is measured in Hz. Defaults to ‘density’

axis : int, optional

Axis along which the spectrogram is computed; the default is over the last axis (i.e. axis=-1).

Returns:

f : ndarray

Array of sample frequencies.

t : ndarray

Array of segment times.

Sxx : ndarray

Spectrogram of x. By default, the last axis of Sxx corresponds to the segment times.

See also

periodogram

Simple, optionally modified periodogram

lombscargle

Lomb-Scargle periodogram for unevenly sampled data

welch

Power spectral density by Welch’s method.

csd

Cross spectral density by Welch’s method.

Notes

An appropriate amount of overlap will depend on the choice of window and on your requirements. In contrast to welch’s method, where the entire data stream is averaged over, one may wish to use a smaller overlap (or perhaps none at all) when computing a spectrogram, to maintain some statistical independence between individual segments.

New in version 0.16.0.

References

...[1] Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time

Signal Processing”, Prentice Hall, 1999.

Examples

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

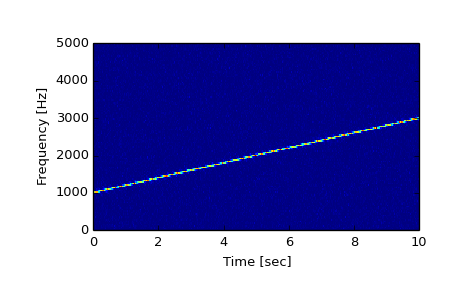
Generate a test signal, a 2 Vrms sine wave whose frequency linearly changes with time from 1kHz to 2kHz, corrupted by 0.001 V**2/Hz of white noise sampled at 10 kHz.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> freq = np.linspace(1e3, 2e3, N)
>>> x = amp * np.sin(2*np.pi*freq*time)
>>> x += np.random.normal(scale=np.sqrt(noise_power), size=time.shape)

Compute and plot the spectrogram.

>>> f, t, Sxx = signal.spectrogram(x, fs)
>>> plt.pcolormesh(t, f, Sxx)
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.show()

(Source code)