scipy.signal.freqz

scipy.signal.freqz(b, a=1, worN=None, whole=0, plot=None)

Compute the frequency response of a digital filter.

Given the numerator b and denominator a of a digital filter, compute its frequency response:

          jw               -jw            -jmw
   jw  B(e)    b[0] + b[1]e + .... + b[m]e
H(e) = ---- = ------------------------------------
          jw               -jw            -jnw
       A(e)    a[0] + a[1]e + .... + a[n]e

Parameters :

b : ndarray

numerator of a linear filter

a : ndarray

denominator of a linear filter

worN : {None, int}, optional

If None, then compute at 512 frequencies around the unit circle. If a single integer, then compute at that many frequencies. Otherwise, compute the response at frequencies given in worN

whole : bool, optional

Normally, frequencies are computed from 0 to pi (upper-half of unit-circle). If whole is True, compute frequencies from 0 to 2*pi.

plot : callable

A callable that takes two arguments. If given, the return parameters w and h are passed to plot. Useful for plotting the frequency response inside freqz.

Returns :

w : ndarray

The frequencies at which h was computed.

h : ndarray

The frequency response.

Notes

Using Matplotlib’s “plot” function as the callable for plot produces unexpected results, this plots the real part of the complex transfer function, not the magnitude.

Examples

>>> from scipy import signal
>>> b = signal.firwin(80, 0.5, window=('kaiser', 8))
>>> w, h = signal.freqz(b)

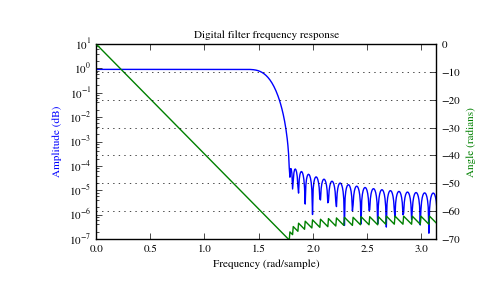
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> plt.title('Digital filter frequency response')
>>> ax1 = fig.add_subplot(111)

>>> plt.semilogy(w, np.abs(h), 'b')
>>> plt.ylabel('Amplitude (dB)', color='b')
>>> plt.xlabel('Frequency (rad/sample)')

>>> ax2 = ax1.twinx()
>>> angles = np.unwrap(np.angle(h))
>>> plt.plot(w, angles, 'g')
>>> plt.ylabel('Angle (radians)', color='g')
>>> plt.grid()
>>> plt.axis('tight')
>>> plt.show()

(Source code)