numpy.polynomial.hermite.hermval

numpy.polynomial.hermite.hermval(x, c, tensor=True)

Evaluate an Hermite series at points x.

If c is of length n + 1, this function returns the value:

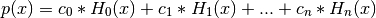
The parameter x is converted to an array only if it is a tuple or a list, otherwise it is treated as a scalar. In either case, either x or its elements must support multiplication and addition both with themselves and with the elements of c.

If c is a 1-D array, then p(x) will have the same shape as x. If c is multidimensional, then the shape of the result depends on the value of tensor. If tensor is true the shape will be c.shape[1:] + x.shape. If tensor is false the shape will be c.shape[1:]. Note that scalars have shape (,).

Trailing zeros in the coefficients will be used in the evaluation, so they should be avoided if efficiency is a concern.

Parameters :

x : array_like, compatible object

If x is a list or tuple, it is converted to an ndarray, otherwise it is left unchanged and treated as a scalar. In either case, x or its elements must support addition and multiplication with with themselves and with the elements of c.

c : array_like

Array of coefficients ordered so that the coefficients for terms of degree n are contained in c[n]. If c is multidimensional the remaining indices enumerate multiple polynomials. In the two dimensional case the coefficients may be thought of as stored in the columns of c.

tensor : boolean, optional

If True, the shape of the coefficient array is extended with ones on the right, one for each dimension of x. Scalars have dimension 0 for this action. The result is that every column of coefficients in c is evaluated for every element of x. If False, x is broadcast over the columns of c for the evaluation. This keyword is useful when c is multidimensional. The default value is True.

New in version 1.7.0.

Returns :

values : ndarray, algebra_like

The shape of the return value is described above.

See also

hermval2d, hermgrid2d, hermval3d, hermgrid3d

Notes

The evaluation uses Clenshaw recursion, aka synthetic division.

Examples

>>> from numpy.polynomial.hermite import hermval
>>> coef = [1,2,3]
>>> hermval(1, coef)
11.0
>>> hermval([[1,2],[3,4]], coef)
array([[  11.,   51.],
       [ 115.,  203.]])