numpy.sinc

numpy.sinc(x)

Return the sinc function.

The sinc function is .

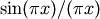Parameters:

x : ndarray

Array (possibly multi-dimensional) of values for which to to calculate sinc(x).

Returns:

out : ndarray

sinc(x), which has the same shape as the input.

Notes

sinc(0) is the limit value 1.

The name sinc is short for “sine cardinal” or “sinus cardinalis”.

The sinc function is used in various signal processing applications, including in anti-aliasing, in the construction of a Lanczos resampling filter, and in interpolation.

For bandlimited interpolation of discrete-time signals, the ideal interpolation kernel is proportional to the sinc function.

References

[R270]

Weisstein, Eric W. “Sinc Function.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/SincFunction.html

[R271]

Wikipedia, “Sinc function”, http://en.wikipedia.org/wiki/Sinc_function

Examples

>>> x = np.arange(-20., 21.)/5.
>>> np.sinc(x)
array([ -3.89804309e-17,  -4.92362781e-02,  -8.40918587e-02,
        -8.90384387e-02,  -5.84680802e-02,   3.89804309e-17,
         6.68206631e-02,   1.16434881e-01,   1.26137788e-01,
         8.50444803e-02,  -3.89804309e-17,  -1.03943254e-01,
        -1.89206682e-01,  -2.16236208e-01,  -1.55914881e-01,
         3.89804309e-17,   2.33872321e-01,   5.04551152e-01,
         7.56826729e-01,   9.35489284e-01,   1.00000000e+00,
         9.35489284e-01,   7.56826729e-01,   5.04551152e-01,
         2.33872321e-01,   3.89804309e-17,  -1.55914881e-01,
        -2.16236208e-01,  -1.89206682e-01,  -1.03943254e-01,
        -3.89804309e-17,   8.50444803e-02,   1.26137788e-01,
         1.16434881e-01,   6.68206631e-02,   3.89804309e-17,
        -5.84680802e-02,  -8.90384387e-02,  -8.40918587e-02,
        -4.92362781e-02,  -3.89804309e-17])

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, np.sinc(x))
>>> plt.title("Sinc Function")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("X")
>>> plt.show()

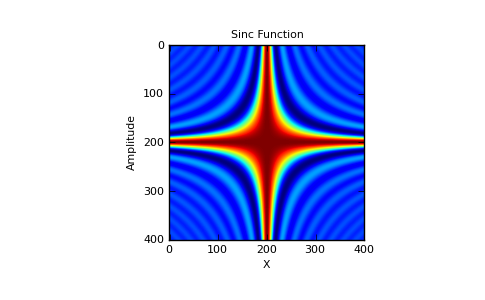
It works in 2-D as well:

>>> x = np.arange(-200., 201.)/50.
>>> xx = np.outer(x, x)
>>> plt.imshow(np.sinc(xx))

(Source code)

Output

(png, pdf)