numpy.random.vonmises¶
- numpy.random.vonmises(mu=0.0, kappa=1.0, size=None)¶
Draw samples from a von Mises distribution.
Samples are drawn from a von Mises distribution with specified mode (mu) and dispersion (kappa), on the interval [-pi, pi].
The von Mises distribution (also known as the circular normal distribution) is a continuous probability distribution on the circle. It may be thought of as the circular analogue of the normal distribution.
Parameters: mu : float
Mode (“center”) of the distribution.
kappa : float, >= 0.
Dispersion of the distribution.
size : {tuple, int}
Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.
Returns: samples : {ndarray, scalar}
The returned samples live on the unit circle [-pi, pi].
See also
- scipy.stats.distributions.vonmises
- probability density function, distribution or cumulative density function, etc.
Notes
The probability density for the von Mises distribution is
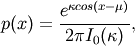
where
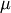 is the mode and
is the mode and 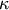 the dispersion,
and
the dispersion,
and  is the modified Bessel function of order 0.
is the modified Bessel function of order 0.The von Mises, named for Richard Edler von Mises, born in Austria-Hungary, in what is now the Ukraine. He fled to the United States in 1939 and became a professor at Harvard. He worked in probability theory, aerodynamics, fluid mechanics, and philosophy of science.
References
[R257] Abramowitz, M. and Stegun, I. A. (ed.), Handbook of Mathematical Functions, National Bureau of Standards, 1964; reprinted Dover Publications, 1965. [R258] von Mises, Richard, 1964, Mathematical Theory of Probability and Statistics (New York: Academic Press). [R259] Wikipedia, “Von Mises distribution”, http://en.wikipedia.org/wiki/Von_Mises_distribution Examples
