numpy.random.standard_t

numpy.random.standard_t(df, size=None)

Standard Student’s t distribution with df degrees of freedom.

A special case of the hyperbolic distribution. As df gets large, the result resembles that of the standard normal distribution (standard_normal).

Parameters:

df : int

Degrees of freedom, should be > 0.

size : int or tuple of ints, optional

Output shape. Default is None, in which case a single value is returned.

Returns:

samples : ndarray or scalar

Drawn samples.

Notes

The probability density function for the t distribution is

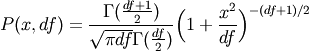
The t test is based on an assumption that the data come from a Normal distribution. The t test provides a way to test whether the sample mean (that is the mean calculated from the data) is a good estimate of the true mean.

The derivation of the t-distribution was forst published in 1908 by William Gisset while working for the Guinness Brewery in Dublin. Due to proprietary issues, he had to publish under a pseudonym, and so he used the name Student.

References

[R255]

Dalgaard, Peter, “Introductory Statistics With R”, Springer, 2002.

[R256]

Wikipedia, “Student’s t-distribution” http://en.wikipedia.org/wiki/Student’s_t-distribution

Examples