numpy.random.mtrand.RandomState.uniform

RandomState.uniform(low=0.0, high=1.0, size=1)

Draw samples from a uniform distribution.

Samples are uniformly distributed over the half-open interval [low, high) (includes low, but excludes high). In other words, any value within the given interval is equally likely to be drawn by uniform.

Parameters:

low : float, optional

Lower boundary of the output interval. All values generated will be greater than or equal to low. The default value is 0.

high : float

Upper boundary of the output interval. All values generated will be less than high. The default value is 1.0.

size : tuple of ints, int, optional

Shape of output. If the given size is, for example, (m,n,k), m*n*k samples are generated. If no shape is specified, a single sample is returned.

Returns:

out : ndarray

Drawn samples, with shape size.

See also

randint

Discrete uniform distribution, yielding integers.

random_integers

Discrete uniform distribution over the closed interval [low, high].

random_sample

Floats uniformly distributed over [0, 1).

random

Alias for random_sample.

rand

Convenience function that accepts dimensions as input, e.g., rand(2,2) would generate a 2-by-2 array of floats, uniformly distributed over [0, 1).

Notes

The probability density function of the uniform distribution is

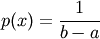
anywhere within the interval [a, b), and zero elsewhere.

Examples

Draw samples from the distribution:

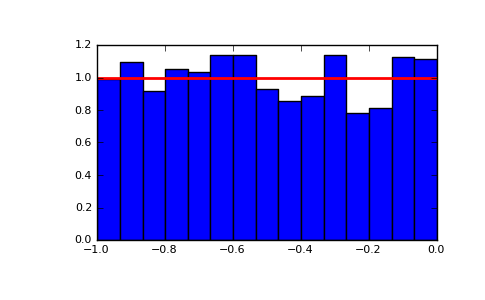
>>> s = np.random.uniform(-1,0,1000)

All values are within the given interval:

>>> np.all(s >= -1)
True

>>> np.all(s < 0)
True

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 15, normed=True)
>>> plt.plot(bins, np.ones_like(bins), linewidth=2, color='r')
>>> plt.show()

(Source code)

Output

(png, pdf)