numpy.arctan

numpy.arctan(x[, out])

Trigonometric inverse tangent, element-wise.

The inverse of tan, so that if y = tan(x) then x = arctan(y).

Parameters:

x : array_like

Input values. arctan is applied to each element of x.

Returns:

out : ndarray

Out has the same shape as x. Its real part is in [-pi/2, pi/2]. It is a scalar if x is a scalar.

See also

arctan2

Calculate the arctan of y/x.

Notes

arctan is a multivalued function: for each x there are infinitely many numbers z such that tan(z) = x. The convention is to return the angle z whose real part lies in [-pi/2, pi/2].

For real-valued input data types, arctan always returns real output. For each value that cannot be expressed as a real number or infinity, it yields nan and sets the invalid floating point error flag.

For complex-valued input, arctan is a complex analytical function that has branch cuts [1j, infj] and [-1j, -infj] and is continuous from the left on the former and from the right on the latter.

The inverse tangent is also known as atan or tan^-1.

References

[R10]

M. Abramowitz and I.A. Stegun, “Handbook of Mathematical Functions”, 10th printing, 1964, pp. 79. http://www.math.sfu.ca/~cbm/aands/

[R11]

Wikipedia, “Inverse trigonometric function”, http://en.wikipedia.org/wiki/Arctan

Examples

We expect the arctan of 0 to be 0, and of 1 to be :

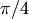>>> np.arctan([0, 1])
array([ 0.        ,  0.78539816])

>>> np.pi/4
0.78539816339744828

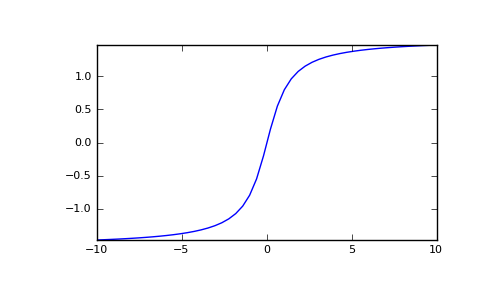
Plot arctan:

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-10, 10)
>>> plt.plot(x, np.arctan(x))
>>> plt.axis('tight')
>>> plt.show()

(Source code)

Output

(png, pdf)