Universal functions (ufunc)

A universal function (or ufunc for short) is a function that operates on ndarrays in an element-by-element fashion, supporting array broadcasting, type casting, and several other standard features. That is, a ufunc is a “vectorized” wrapper for a function that takes a fixed number of scalar inputs and produces a fixed number of scalar outputs.

In Numpy, universal functions are instances of the numpy.ufunc class. Many of the built-in functions are implemented in compiled C code, but ufunc instances can also be produced using the frompyfunc factory function.

Broadcasting

Each universal function takes array inputs and produces array outputs by performing the core function element-wise on the inputs. Standard broadcasting rules are applied so that inputs not sharing exactly the same shapes can still be usefully operated on. Broadcasting can be understood by four rules:

1. All input arrays with ndim smaller than the input array of largest ndim have 1’s prepended to their shapes.
2. The size in each dimension of the output shape is the maximum of all the input shapes in that dimension.
3. An input can be used in the calculation if it’s shape in a particular dimension either matches the output shape or has value exactly 1.
4. If an input has a dimension size of 1 in its shape, the first data entry in that dimension will be used for all calculations along that dimension. In other words, the stepping machinery of the ufunc will simply not step along that dimension when otherwise needed (the stride will be 0 for that dimension).

Broadcasting is used throughout NumPy to decide how to handle non equally-shaped arrays; for example all arithmetic operators (+, -, *, ...) between ndarrays broadcast the arrays before operation.

A set of arrays is called “broadcastable” to the same shape if the above rules produce a valid result, i.e., one of the following is true:

1. The arrays all have exactly the same shape.
2. The arrays all have the same number of dimensions and the length of each dimensions is either a common length or 1.
3. The arrays that have too few dimensions can have their shapes prepended with a dimension of length 1 to satisfy property 2.

Example

If a.shape is (5,1), b.shape is (1,6), c.shape is (6,) and d.shape is () so that d is a scalar, then a, b, c, and d are all broadcastable to dimension (5,6); and

• a acts like a (5,6) array where a[:,0] is broadcast to the other columns,
• b acts like a (5,6) array where b[0,:] is broadcast to the other rows,
• c acts like a (1,6) array and therefore like a (5,6) array where ``c[:]` is broadcast to every row, and finally,
• d acts like a (5,6) array where the single value is repeated.

Output type determination

The output of the ufunc (and its methods) is not necessarily an ndarray, if all input arguments are not ndarrays.

All output arrays will be passed to the __array_wrap__ method of the input (besides ndarrays, and scalars) that defines it and has the highest __array_priority__ of any other input to the universal function. The default __array_priority__ of the ndarray is 0.0, and the default __array_priority__ of a subtype is 1.0. Matrices have __array_priority__ equal to 10.0.

The ufuncs can also all take output arguments. The output will be cast if necessary to the provided output array. If a class with an __array__ method is used for the output, results will be written to the object returned by __array__. Then, if the class also has an __array_wrap__ method, the returned ndarray result will be passed to that method just before passing control back to the caller.

Use of internal buffers

Internally, buffers are used for misaligned data, swapped data, and data that has to be converted from one data type to another. The size of the internal buffers is settable on a per-thread basis. There can be up to 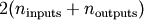buffers of the specified size created to handle the data from all the inputs and outputs of a ufunc. The default size of the buffer is 10,000 elements. Whenever buffer-based calculation would be needed, but all input arrays are smaller than the buffer size, those misbehaved or incorrect typed arrays will be copied before the calculation proceeds. Adjusting the size of the buffer may therefore alter the speed at which ufunc calculations of various sorts are completed. A simple interface for setting this variable is accessible using the function

setbufsize (size)

Set the size of the buffer used in ufuncs.

Error handling

Universal functions can trip special floating point status registers in your hardware (such as divide-by-zero). If available on your platform, these registers will be regularly checked during calculation. Error handling is controlled on a per-thread basis, and can be configured using the functions

seterr ([all, divide, over, ...])	Set how floating-point errors are handled.
seterrcall (func)	Set the floating-point error callback function or log object.

Casting Rules

At the core of every ufunc is a one-dimensional strided loop that implements the actual function for a specific type combination. When a ufunc is created, it is given a static list of inner loops and a corresponding list of type signatures over which the ufunc operates. The ufunc machinery uses this list to determine which inner loop to use for a particular case. You can inspect the .types attribute for a particular ufunc to see which type combinations have a defined inner loop and which output type they produce (character codes are used in that output for brevity).

Casting must be done on one or more of the inputs whenever the ufunc does not have a core loop implementation for the input types provided. If an implementation for the input types cannot be found, then the algorithm searches for an implementation with a type signature to which all of the inputs can be cast “safely.” The first one it finds in its internal list of loops is selected and performed with types cast. Recall that internal copies during ufuncs (even for casting) are limited to the size of an internal buffer which is user settable.

Note

Universal functions in NumPy are flexible enough to have mixed type signatures. Thus, for example, a universal function could be defined that works with floating point and integer values. See ldexp for an example.

By the above description, the casting rules are essentially implemented by the question of when a data type can be cast “safely” to another data type. The answer to this question can be determined in Python with a function call: can_cast(fromtype, totype). Figure shows the results of this call for my 32-bit system on the 21 internally supported types. You can generate this table for your system with code shown in that Figure.

Figure

Code segment showing the can cast safely table for a 32-bit system.

>>> def print_table(ntypes):
...     print 'X',
...     for char in ntypes: print char,
...     print
...     for row in ntypes:
...         print row,
...         for col in ntypes:
...             print int(np.can_cast(row, col)),
...         print
>>> print_table(np.typecodes['All'])
X ? b h i l q p B H I L Q P f d g F D G S U V O
? 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
b 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1
h 0 0 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1
i 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
l 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
q 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
p 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
B 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
H 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
I 0 0 0 0 0 1 0 0 0 1 1 1 1 0 1 1 0 1 1 1 1 1 1
L 0 0 0 0 0 1 0 0 0 1 1 1 1 0 1 1 0 1 1 1 1 1 1
Q 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 1 1 1
P 0 0 0 0 0 1 0 0 0 1 1 1 1 0 1 1 0 1 1 1 1 1 1
f 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1
d 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
g 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1
F 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1
D 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1
G 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1
S 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
U 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
V 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
O 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1

You should note that, while included in the table for completeness, the ‘S’, ‘U’, and ‘V’ types cannot be operated on by ufuncs. Also, note that on a 64-bit system the integer types may have different sizes resulting in a slightly altered table.

Mixed scalar-array operations use a different set of casting rules that ensure that a scalar cannot upcast an array unless the scalar is of a fundamentally different kind of data (i.e. under a different hierachy in the data type hierarchy) than the array. This rule enables you to use scalar constants in your code (which as Python types are interpreted accordingly in ufuncs) without worrying about whether the precision of the scalar constant will cause upcasting on your large (small precision) array.

ufunc

Optional keyword arguments

All ufuncs take optional keyword arguments. These represent rather advanced usage and will likely not be used by most users.

sig

Either a data-type, a tuple of data-types, or a special signature string indicating the input and output types of a ufunc. This argument allows you to specify a specific signature for a the 1-d loop to use in the underlying calculation. If the loop specified does not exist for the ufunc, then a TypeError is raised. Normally a suitable loop is found automatically by comparing the input types with what is available and searching for a loop with data-types to which all inputs can be cast safely. This key-word argument lets you by-pass that search and choose a loop you want. A list of available signatures is available in the types attribute of the ufunc object.

extobj

a list of length 1, 2, or 3 specifying the ufunc buffer-size, the error mode integer, and the error call-back function. Normally, these values are looked-up in a thread-specific dictionary. Passing them here bypasses that look-up and uses the low-level specification provided for the error-mode. This may be useful as an optimization for calculations requiring lots of ufuncs on small arrays in a loop.

Attributes

There are some informational attributes that universal functions possess. None of the attributes can be set.

__doc__	A docstring for each ufunc. The first part of the docstring is dynamically generated from the number of outputs, the name, and the number of inputs. The second part of the doc string is provided at creation time and stored with the ufunc.
__name__	The name of the ufunc.

ufunc.nin	number of inputs
ufunc.nout	number of outputs
ufunc.nargs	number of arguments
ufunc.ntypes	number of types
ufunc.types	return a list with types grouped input->output
ufunc.identity	identity value

Methods

All ufuncs have 4 methods. However, these methods only make sense on ufuncs that take two input arguments and return one output argument. Attempting to call these methods on other ufuncs will cause a ValueError . The reduce-like methods all take an axis keyword and a dtype keyword, and the arrays must all have dimension >= 1. The axis keyword specifies which axis of the array the reduction will take place over and may be negative, but must be an integer. The dtype keyword allows you to manage a very common problem that arises when naively using {op}.reduce. Sometimes you may have an array of a certain data type and wish to add up all of its elements, but the result does not fit into the data type of the array. This commonly happens if you have an array of single-byte integers. The dtype keyword allows you to alter the data type that the reduction takes place over (and therefore the type of the output). Thus, you can ensure that the output is a data type with large-enough precision to handle your output. The responsibility of altering the reduce type is mostly up to you. There is one exception: if no dtype is given for a reduction on the “add” or “multiply” operations, then if the input type is an integer (or boolean) data- type and smaller than the size of the int_ data type, it will be internally upcast to the int_ (or uint) data type.

ufunc.reduce (array[, axis, dtype, out])	Reduce applies the operator to all elements of the array.
ufunc.accumulate (array[, axis, dtype, out])	Accumulate the result of applying the operator to all elements.
ufunc.reduceat (self, array, indices[, axis, dtype, out])	Reduceat performs a reduce with specified slices over an axis.
ufunc.outer (A,B)	Compute the result of applying op to all pairs (a,b)

Warning

A reduce-like operation on an array with a data type that has range “too small “to handle the result will silently wrap. You should use dtype to increase the data type over which reduction takes place.

Available ufuncs

There are currently more than 60 universal functions defined in numpy on one or more types, covering a wide variety of operations. Some of these ufuncs are called automatically on arrays when the relevant infix notation is used (e.g. add(a, b) is called internally when a + b is written and a or b is an ndarray). Nonetheless, you may still want to use the ufunc call in order to use the optional output argument(s) to place the output(s) in an object (or in objects) of your choice.

Recall that each ufunc operates element-by-element. Therefore, each ufunc will be described as if acting on a set of scalar inputs to return a set of scalar outputs.

Note

The ufunc still returns its output(s) even if you use the optional output argument(s).

Math operations

add (x1, x2[, out])	Add arguments element-wise.
subtract (x1, x2[, out])	Subtract arguments element-wise.
multiply (x1, x2[, out])	Multiply arguments elementwise.
divide (x1, x2[, out])	Divide arguments element-wise.
logaddexp (x1, x2[, out])	Logarithm of exp(x) + exp(y).
logaddexp2 (x1, x2[, out])	Base-2 Logarithm of 2**x + 2**y.
true_divide (x1, x2[, out])	Returns an element-wise, true division of the inputs.
floor_divide (x1, x2[, out])	Return the largest integer smaller or equal to the division of the inputs.
negative (x[, out])	Returns an array with the negative of each element of the original array.
power (x1, x2[, out])	Returns element-wise base array raised to power from second array.
remainder (x1, x2[, out])	Returns element-wise remainder of division.
mod (x1, x2[, out])	Returns element-wise remainder of division.
fmod (x1, x2[, out])	Return the remainder of division.
absolute (x[, out])	Calculate the absolute value element-wise.
rint (x[, out])	Round elements of the array to the nearest integer.
sign (x[, out])	Returns an element-wise indication of the sign of a number.
conj (x[, out])	Return the complex conjugate, element-wise.
exp (x[, out])	Calculate the exponential of the elements in the input array.
exp2 (x[, out])	Calculate 2**p for all p in the input array.
log (x[, out])	Natural logarithm, element-wise.
log2 (x[, y])	Return the base 2 logarithm.
log10 (x[, out])	Compute the logarithm in base 10 element-wise.
expm1 (x[, out])	Return the exponential of the elements in the array minus one.
log1p (x[, out])	log(1 + x) in base e, elementwise.
sqrt (x[, out])	Return the positive square-root of an array, element-wise.
square (x[, out])	Return the element-wise square of the input.
reciprocal (x[, out])	Return element-wise reciprocal.
ones_like (x[, out])	Returns an array of ones with the same shape and type as a given array.

Tip

The optional output arguments can be used to help you save memory for large calculations. If your arrays are large, complicated expressions can take longer than absolutely necessary due to the creation and (later) destruction of temporary calculation spaces. For example, the expression G=a*b+c is equivalent to t1=A*B; G=T1+C; del t1. It will be more quickly executed as G=A*B; add(G,C,G) which is the same as G=A*B; G+=C.

Trigonometric functions

All trigonometric functions use radians when an angle is called for. The ratio of degrees to radians is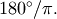

sin (x[, out])	Trigonometric sine, element-wise.
cos (x[, out])	Cosine elementwise.
tan (x[, out])	Compute tangent element-wise.
arcsin (x[, out])	Inverse sine elementwise.
arccos (x[, out])	Trigonometric inverse cosine, element-wise.
arctan (x[, out])	Trigonometric inverse tangent, element-wise.
arctan2 (x1, x2[, out])	Elementwise arc tangent of x1/x2 choosing the quadrant correctly.
hypot (x1, x2[, out])	Given two sides of a right triangle, return its hypotenuse.
sinh (x[, out])	Hyperbolic sine, element-wise.
cosh (x[, out])	Hyperbolic cosine, element-wise.
tanh (x[, out])	Hyperbolic tangent element-wise.
arcsinh (x[, out])	Inverse hyperbolic sine elementwise.
arccosh (x[, out])	Inverse hyperbolic cosine, elementwise.
arctanh (x[, out])	Inverse hyperbolic tangent elementwise.
deg2rad (x[, out])	Convert angles from degrees to radians. This is the same function as radians, but deg2rad is a more descriptive name.
rad2deg (x[, out])	Convert angles from radians to degrees. This is the same function as degrees but is preferred because its more descriptive name.

Bit-twiddling functions

These function all need integer arguments and they maniuplate the bit- pattern of those arguments.

bitwise_and (x1, x2[, out])	Compute bit-wise AND of two arrays, element-wise.
bitwise_or (x1, x2[, out])	Compute bit-wise OR of two arrays, element-wise.
bitwise_xor (x1, x2[, out])	Compute bit-wise XOR of two arrays, element-wise.
invert (x[, out])	Compute bit-wise inversion, or bit-wise NOT, element-wise.
left_shift (x1, x2[, out])	Shift the bits of an integer to the left.
right_shift (x1, x2[, out])	Shift the bits of an integer to the right.

Comparison functions

greater (x1, x2[, out])	Return (x1 > x2) element-wise.
greater_equal (x1, x2[, out])	Element-wise True if first array is greater or equal than second array.
less (x1, x2[, out])	Returns (x1 < x2) element-wise.
less_equal (x1, x2[, out])	Returns (x1 <= x2) element-wise.
not_equal (x1, x2[, out])	Return (x1 != x2) element-wise.
equal (x1, x2[, out])	Returns elementwise x1 == x2 in a bool array.

Warning

Do not use the Python keywords and and or to combine logical array expressions. These keywords will test the truth value of the entire array (not element-by-element as you might expect). Use the bitwise operators: & and | instead.

logical_and (x1, x2[, out])	Compute the truth value of x1 AND x2 elementwise.
logical_or (x1, x2[, out])	Compute the truth value of x1 OR x2 elementwise.
logical_xor (x1, x2[, out])	Compute the truth value of x1 XOR x2 elementwise.
logical_not (x[, out])	Compute the truth value of NOT x elementwise.

Warning

The Bitwise operators (& and |) are the proper way to combine element-by-element array comparisons. Be sure to understand the operator precedence: (a>2) & (a<5) is the proper syntax because a>2 & a<5 will result in an error due to the fact that 2 & a is evaluated first.

maximum (x1, x2[, out])

Element-wise maximum of array elements.

Tip

The Python function max() will find the maximum over a one-dimensional array, but it will do so using a slower sequence interface. The reduce method of the maximum ufunc is much faster. Also, the max() method will not give answers you might expect for arrays with greater than one dimension. The reduce method of minimum also allows you to compute a total minimum over an array.

minimum (x1, x2[, out])

Element-wise minimum of array elements.

Warning

the behavior of maximum(a,b) is than that of max(a,b). As a ufunc, maximum(a,b) performs an element-by-element comparison of a and b and chooses each element of the result according to which element in the two arrays is larger. In contrast, max(a,b) treats the objects a and b as a whole, looks at the (total) truth value of a>b and uses it to return either a or b (as a whole). A similar difference exists between minimum(a,b) and min(a,b).

Floating functions

Recall that all of these functions work element-by-element over an array, returning an array output. The description details only a single operation.

isreal (x)	Returns a bool array where True if the corresponding input element is real.
iscomplex (x)	Return a bool array, True if element is complex (non-zero imaginary part).
isfinite (x[, out])	Returns True for each element that is a finite number.
isinf (x[, out])	Shows which elements of the input are positive or negative infinity. Returns a numpy boolean scalar or array resulting from an element-wise test for positive or negative infinity.
isnan (x[, out])	Returns a numpy boolean scalar or array resulting from an element-wise test for Not a Number (NaN).
signbit (x[, out])	Returns element-wise True where signbit is set (less than zero).
modf (x[, out1, out2])	Return the fractional and integral part of a number.
ldexp (x1, x2[, out])	Compute y = x1 * 2**x2.
frexp (x[, out1, out2])	Split the number, x, into a normalized fraction (y1) and exponent (y2)
fmod (x1, x2[, out])	Return the remainder of division.
floor (x[, out])	Return the floor of the input, element-wise.
ceil (x[, out])	Return the ceiling of the input, element-wise.
trunc (x[, out])	Return the truncated value of the input, element-wise.