numpy.bitwise_and

numpy.bitwise_and(x1, x2[, out])

Compute bit-wise AND of two arrays, element-wise.

When calculating the bit-wise AND between two elements, x and y, each element is first converted to its binary representation (which works just like the decimal system, only now we’re using 2 instead of 10):

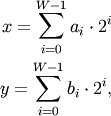
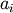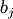where W is the bit-width of the type (i.e., 8 for a byte or uint8), and each and is either 0 or 1. For example, 13 is represented as 00001101, which translates to .

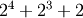The bit-wise operator is the result of

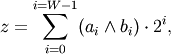
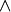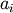where is the AND operator, which yields one whenever both and 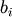are 1.

Parameters:

x1, x2 : array_like

Only integer types are handled (including booleans).

Returns:

out : array_like

Result.

See also

bitwise_or, bitwise_xor, logical_and

binary_repr

Return the binary representation of the input number as a string.

Examples

We’ve seen that 13 is represented by 00001101. Similary, 17 is represented by 00010001. The bit-wise AND of 13 and 17 is therefore 000000001, or 1:

>>> np.bitwise_and(13, 17)
1

>>> np.bitwise_and(14, 13)
12
>>> np.binary_repr(12)
'1100'
>>> np.bitwise_and([14,3], 13)
array([12,  1])

>>> np.bitwise_and([11,7], [4,25])
array([0, 1])
>>> np.bitwise_and(np.array([2,5,255]), np.array([3,14,16]))
array([ 2,  4, 16])
>>> np.bitwise_and([True, True], [False, True])
array([False,  True], dtype=bool)