root#
- scipy.optimize.root(fun, x0, args=(), method='hybr', jac=None, tol=None, callback=None, options=None)[source]#
Find a root of a vector function.
- Parameters:
- funcallable
A vector function to find a root of.
Suppose the callable has signature
f0(x, *my_args, **my_kwargs), wheremy_argsandmy_kwargsare required positional and keyword arguments. Rather than passingf0as the callable, wrap it to accept onlyx; e.g., passfun=lambda x: f0(x, *my_args, **my_kwargs)as the callable, wheremy_args(tuple) andmy_kwargs(dict) have been gathered before invoking this function.- x0ndarray
Initial guess.
- argstuple, optional
Extra arguments passed to the objective function and its Jacobian.
- methodstr, optional
Type of solver. Should be one of
‘hybr’ (see here)
‘lm’ (see here)
‘broyden1’ (see here)
‘broyden2’ (see here)
‘anderson’ (see here)
‘linearmixing’ (see here)
‘diagbroyden’ (see here)
‘excitingmixing’ (see here)
‘krylov’ (see here)
‘df-sane’ (see here)
- jacbool or callable, optional
If jac is a Boolean and is True, fun is assumed to return the value of Jacobian along with the objective function. If False, the Jacobian will be estimated numerically. jac can also be a callable returning the Jacobian of fun. In this case, it must accept the same arguments as fun.
- tolfloat, optional
Tolerance for termination. For detailed control, use solver-specific options.
- callbackfunction, optional
Optional callback function. It is called on every iteration as
callback(x, f)where x is the current solution and f the corresponding residual. For all methods but ‘hybr’ and ‘lm’.- optionsdict, optional
A dictionary of solver options. E.g., xtol or maxiter, see
show_options()for details.
- Returns:
- solOptimizeResult
The solution represented as a
OptimizeResultobject. Important attributes are:xthe solution array,successa Boolean flag indicating if the algorithm exited successfully andmessagewhich describes the cause of the termination. SeeOptimizeResultfor a description of other attributes.
See also
show_optionsAdditional options accepted by the solvers
Notes
This section describes the available solvers that can be selected by the ‘method’ parameter. The default method is hybr.
Method hybr uses a modification of the Powell hybrid method as implemented in MINPACK [1].
Method lm solves the system of nonlinear equations in a least squares sense using a modification of the Levenberg-Marquardt algorithm as implemented in MINPACK [1].
Method df-sane is a derivative-free spectral method. [3]
Methods broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov are inexact Newton methods, with backtracking or full line searches [2]. Each method corresponds to a particular Jacobian approximations.
Method broyden1 uses Broyden’s first Jacobian approximation, it is known as Broyden’s good method.
Method broyden2 uses Broyden’s second Jacobian approximation, it is known as Broyden’s bad method.
Method anderson uses (extended) Anderson mixing.
Method Krylov uses Krylov approximation for inverse Jacobian. It is suitable for large-scale problem.
Method diagbroyden uses diagonal Broyden Jacobian approximation.
Method linearmixing uses a scalar Jacobian approximation.
Method excitingmixing uses a tuned diagonal Jacobian approximation.
Warning
The algorithms implemented for methods diagbroyden, linearmixing and excitingmixing may be useful for specific problems, but whether they will work may depend strongly on the problem.
Added in version 0.11.0.
References
[1] (1,2)More, Jorge J., Burton S. Garbow, and Kenneth E. Hillstrom. 1980. User Guide for MINPACK-1.
[2]C. T. Kelley. 1995. Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics. DOI:10.1137/1.9781611970944
[3]W. La Cruz, J.M. Martinez, M. Raydan. Math. Comp. 75, 1429 (2006).
Examples
The following functions define a system of nonlinear equations and its jacobian.
>>> import numpy as np >>> def fun(x): ... return [x[0] + 0.5 * (x[0] - x[1])**3 - 1.0, ... 0.5 * (x[1] - x[0])**3 + x[1]]
>>> def jac(x): ... return np.array([[1 + 1.5 * (x[0] - x[1])**2, ... -1.5 * (x[0] - x[1])**2], ... [-1.5 * (x[1] - x[0])**2, ... 1 + 1.5 * (x[1] - x[0])**2]])
A solution can be obtained as follows.
>>> from scipy import optimize >>> sol = optimize.root(fun, [0, 0], jac=jac, method='hybr') >>> sol.x array([ 0.8411639, 0.1588361])
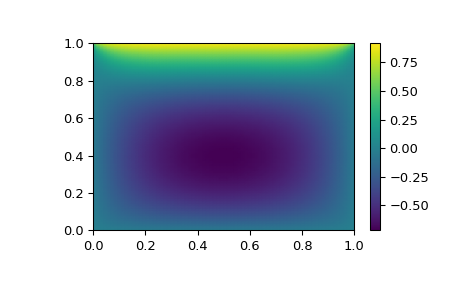
Large problem
Suppose that we needed to solve the following integrodifferential equation on the square \([0,1]\times[0,1]\):
\[\nabla^2 P = 10 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2\]with \(P(x,1) = 1\) and \(P=0\) elsewhere on the boundary of the square.
The solution can be found using the
method='krylov'solver:>>> from scipy import optimize >>> # parameters >>> nx, ny = 75, 75 >>> hx, hy = 1./(nx-1), 1./(ny-1)
>>> P_left, P_right = 0, 0 >>> P_top, P_bottom = 1, 0
>>> def residual(P): ... d2x = np.zeros_like(P) ... d2y = np.zeros_like(P) ... ... d2x[1:-1] = (P[2:] - 2*P[1:-1] + P[:-2]) / hx/hx ... d2x[0] = (P[1] - 2*P[0] + P_left)/hx/hx ... d2x[-1] = (P_right - 2*P[-1] + P[-2])/hx/hx ... ... d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy ... d2y[:,0] = (P[:,1] - 2*P[:,0] + P_bottom)/hy/hy ... d2y[:,-1] = (P_top - 2*P[:,-1] + P[:,-2])/hy/hy ... ... return d2x + d2y - 10*np.cosh(P).mean()**2
>>> guess = np.zeros((nx, ny), float) >>> sol = optimize.root(residual, guess, method='krylov') >>> print('Residual: %g' % abs(residual(sol.x)).max()) Residual: 5.7972e-06 # may vary
>>> import matplotlib.pyplot as plt >>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)] >>> plt.pcolormesh(x, y, sol.x, shading='gouraud') >>> plt.colorbar() >>> plt.show()