lanczos#
- scipy.signal.windows.lanczos(M, *, sym=True, xp=None, device=None)[source]#
Return a Lanczos window also known as a sinc window.
- Parameters:
- Mint
Number of points in the output window. If zero, an empty array is returned. An exception is thrown when it is negative.
- symbool, optional
When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.
- xparray_namespace, optional
Optional array namespace. Should be compatible with the array API standard, or supported by array-api-compat. Default:
numpy- device: any
optional device specification for output. Should match one of the supported device specification in
xp.
- Returns:
- wndarray
The window, with the maximum value normalized to 1 (though the value 1 does not appear if M is even and sym is True).
Notes
The Lanczos window is defined as
\[w(n) = sinc \left( \frac{2n}{M - 1} - 1 \right)\]where
\[sinc(x) = \frac{\sin(\pi x)}{\pi x}\]The Lanczos window has reduced Gibbs oscillations and is widely used for filtering climate timeseries with good properties in the physical and spectral domains.
Added in version 1.10.
Array API Standard Support
lanczoshas experimental support for Python Array API Standard compatible backends in addition to NumPy. Please consider testing these features by setting an environment variableSCIPY_ARRAY_API=1and providing CuPy, PyTorch, JAX, or Dask arrays as array arguments. The following combinations of backend and device (or other capability) are supported.Library
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
✅
JAX
✅
✅
Dask
✅
n/a
See Support for the array API standard for more information.
References
[1]Lanczos, C., and Teichmann, T. (1957). Applied analysis. Physics Today, 10, 44.
[2]Duchon C. E. (1979) Lanczos Filtering in One and Two Dimensions. Journal of Applied Meteorology, Vol 18, pp 1016-1022.
[3]Thomson, R. E. and Emery, W. J. (2014) Data Analysis Methods in Physical Oceanography (Third Edition), Elsevier, pp 593-637.
[4]Wikipedia, “Window function”, http://en.wikipedia.org/wiki/Window_function
Examples
Plot the window
>>> import numpy as np >>> from scipy.signal.windows import lanczos >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1) >>> window = lanczos(51) >>> ax.plot(window) >>> ax.set_title("Lanczos window") >>> ax.set_ylabel("Amplitude") >>> ax.set_xlabel("Sample") >>> fig.tight_layout() >>> plt.show()
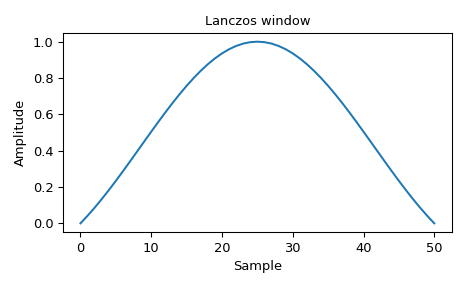
and its frequency response:
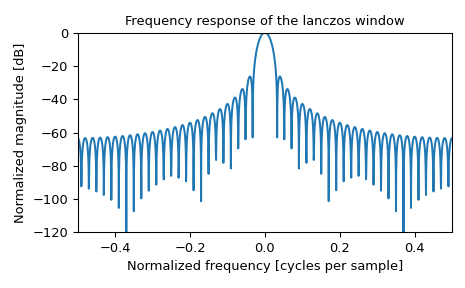
>>> fig, ax = plt.subplots(1) >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> ax.plot(freq, response) >>> ax.set_xlim(-0.5, 0.5) >>> ax.set_ylim(-120, 0) >>> ax.set_title("Frequency response of the lanczos window") >>> ax.set_ylabel("Normalized magnitude [dB]") >>> ax.set_xlabel("Normalized frequency [cycles per sample]") >>> fig.tight_layout() >>> plt.show()