scipy.signal.lp2bs#

scipy.signal.lp2bs(b, a, wo=1.0, bw=1.0)[source]#

Transform a lowpass filter prototype to a bandstop filter.

Return an analog band-stop filter with center frequency wo and bandwidth bw from an analog low-pass filter prototype with unity cutoff frequency, in transfer function (‘ba’) representation.

Parameters

barray_like: Numerator polynomial coefficients.
aarray_like: Denominator polynomial coefficients.
wofloat: Desired stopband center, as angular frequency (e.g., rad/s). Defaults to no change.
bwfloat: Desired stopband width, as angular frequency (e.g., rad/s). Defaults to 1.

Returns

barray_like: Numerator polynomial coefficients of the transformed band-stop filter.
aarray_like: Denominator polynomial coefficients of the transformed band-stop filter.

See also

lp2lp, lp2hp, lp2bp, bilinear
lp2bs_zpk

Notes

This is derived from the s-plane substitution

\[s \rightarrow \frac{s \cdot \mathrm{BW}}{s^2 + {\omega_0}^2}\]

This is the “wideband” transformation, producing a stopband with geometric (log frequency) symmetry about wo.

Examples

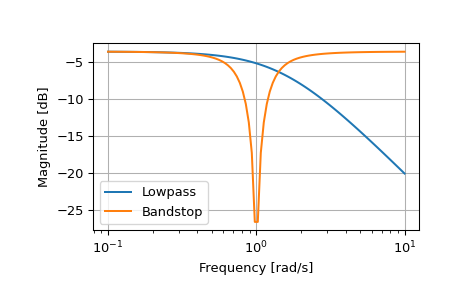
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> lp = signal.lti([1.0], [1.0, 1.5])
>>> bs = signal.lti(*signal.lp2bs(lp.num, lp.den))
>>> w, mag_lp, p_lp = lp.bode()
>>> w, mag_bs, p_bs = bs.bode(w)
>>> plt.plot(w, mag_lp, label='Lowpass')
>>> plt.plot(w, mag_bs, label='Bandstop')
>>> plt.semilogx()
>>> plt.grid(True)
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Magnitude [dB]')
>>> plt.legend()