scipy.stats.siegelslopes

scipy.stats.siegelslopes(y, x=None, method='hierarchical')

Computes the Siegel estimator for a set of points (x, y).

siegelslopes implements a method for robust linear regression using repeated medians (see [1]) to fit a line to the points (x, y). The method is robust to outliers with an asymptotic breakdown point of 50%.

Parameters

yarray_like

Dependent variable.

xarray_like or None, optional

Independent variable. If None, use arange(len(y)) instead.

method{‘hierarchical’, ‘separate’}

If ‘hierarchical’, estimate the intercept using the estimated slope medslope (default option). If ‘separate’, estimate the intercept independent of the estimated slope. See Notes for details.

Returns

medslopefloat

Estimate of the slope of the regression line.

medinterceptfloat

Estimate of the intercept of the regression line.

See also

theilslopes

a similar technique without repeated medians

Notes

With n = len(y), compute m_j as the median of the slopes from the point (x[j], y[j]) to all other n-1 points. medslope is then the median of all slopes m_j. Two ways are given to estimate the intercept in [1] which can be chosen via the parameter method. The hierarchical approach uses the estimated slope medslope and computes medintercept as the median of y - medslope*x. The other approach estimates the intercept separately as follows: for each point (x[j], y[j]), compute the intercepts of all the n-1 lines through the remaining points and take the median i_j. medintercept is the median of the i_j.

The implementation computes n times the median of a vector of size n which can be slow for large vectors. There are more efficient algorithms (see [2]) which are not implemented here.

References

1(1,2)

A. Siegel, “Robust Regression Using Repeated Medians”, Biometrika, Vol. 69, pp. 242-244, 1982.

2

A. Stein and M. Werman, “Finding the repeated median regression line”, Proceedings of the Third Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 409-413, 1992.

Examples

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

Compute the slope and intercept. For comparison, also compute the least-squares fit with linregress:

>>> res = stats.siegelslopes(y, x)
>>> lsq_res = stats.linregress(x, y)

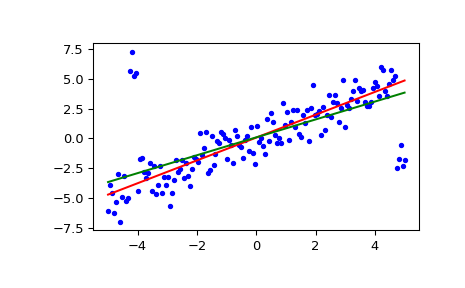
Plot the results. The Siegel regression line is shown in red. The green line shows the least-squares fit for comparison.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()

previous

scipy.stats.linregress

next

scipy.stats.theilslopes