scipy.special.erf#

scipy.special.erf(z) = <ufunc 'erf'>#

Returns the error function of complex argument.

It is defined as 2/sqrt(pi)*integral(exp(-t**2), t=0..z).

Parameters

xndarray: Input array.

Returns

resndarray: The values of the error function at the given points x.

See also

erfc, erfinv, erfcinv, wofz, erfcx, erfi

Notes

The cumulative of the unit normal distribution is given by Phi(z) = 1/2[1 + erf(z/sqrt(2))].

References

1: https://en.wikipedia.org/wiki/Error_function
2: Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. http://www.math.sfu.ca/~cbm/aands/page_297.htm
3: Steven G. Johnson, Faddeeva W function implementation. http://ab-initio.mit.edu/Faddeeva

Examples

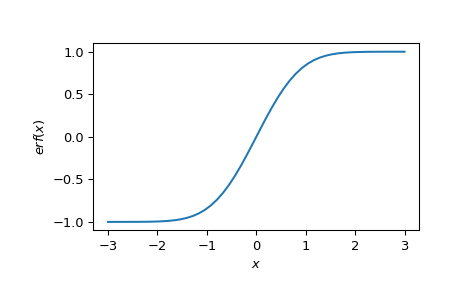
>>> from scipy import special
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-3, 3)
>>> plt.plot(x, special.erf(x))
>>> plt.xlabel('$x$')
>>> plt.ylabel('$erf(x)$')
>>> plt.show()

scipy.special.poch

scipy.special.erfc