scipy.spatial.KDTree.query_ball_tree

KDTree.query_ball_tree(other, r, p=2.0, eps=0)

Find all pairs of points between self and other whose distance is at most r.

Parameters

otherKDTree instance

The tree containing points to search against.

rfloat

The maximum distance, has to be positive.

pfloat, optional

Which Minkowski norm to use. p has to meet the condition 1 <= p <= infinity.

epsfloat, optional

Approximate search. Branches of the tree are not explored if their nearest points are further than r/(1+eps), and branches are added in bulk if their furthest points are nearer than r * (1+eps). eps has to be non-negative.

Returns

resultslist of lists

For each element self.data[i] of this tree, results[i] is a list of the indices of its neighbors in other.data.

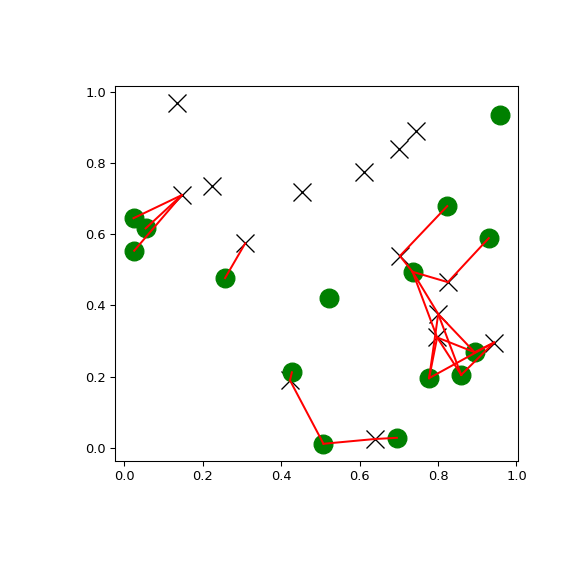
Examples

You can search all pairs of points between two kd-trees within a distance:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.spatial import KDTree
>>> rng = np.random.default_rng()
>>> points1 = rng.random((15, 2))
>>> points2 = rng.random((15, 2))
>>> plt.figure(figsize=(6, 6))
>>> plt.plot(points1[:, 0], points1[:, 1], "xk", markersize=14)
>>> plt.plot(points2[:, 0], points2[:, 1], "og", markersize=14)
>>> kd_tree1 = KDTree(points1)
>>> kd_tree2 = KDTree(points2)
>>> indexes = kd_tree1.query_ball_tree(kd_tree2, r=0.2)
>>> for i in range(len(indexes)):
...     for j in indexes[i]:
...         plt.plot([points1[i, 0], points2[j, 0]],
...             [points1[i, 1], points2[j, 1]], "-r")
>>> plt.show()

scipy.spatial.KDTree.query_ball_point scipy.spatial.KDTree.query_pairs