scipy.interpolate.RBFInterpolator¶
- class scipy.interpolate.RBFInterpolator(y, d, neighbors=None, smoothing=0.0, kernel='thin_plate_spline', epsilon=None, degree=None)[source]¶
Radial basis function (RBF) interpolation in N dimensions.
- Parameters
- y(P, N) array_like
Data point coordinates.
- d(P, …) array_like
Data values at y.
- neighborsint, optional
If specified, the value of the interpolant at each evaluation point will be computed using only this many nearest data points. All the data points are used by default.
- smoothingfloat or (P,) array_like, optional
Smoothing parameter. The interpolant perfectly fits the data when this is set to 0. For large values, the interpolant approaches a least squares fit of a polynomial with the specified degree. Default is 0.
- kernelstr, optional
Type of RBF. This should be one of
‘linear’ :
-r‘thin_plate_spline’ :
r**2 * log(r)‘cubic’ :
r**3‘quintic’ :
-r**5‘multiquadric’ :
-sqrt(1 + r**2)‘inverse_multiquadric’ :
1/sqrt(1 + r**2)‘inverse_quadratic’ :
1/(1 + r**2)‘gaussian’ :
exp(-r**2)
Default is ‘thin_plate_spline’.
- epsilonfloat, optional
Shape parameter that scales the input to the RBF. If kernel is ‘linear’, ‘thin_plate_spline’, ‘cubic’, or ‘quintic’, this defaults to 1 and can be ignored because it has the same effect as scaling the smoothing parameter. Otherwise, this must be specified.
- degreeint, optional
Degree of the added polynomial. For some RBFs the interpolant may not be well-posed if the polynomial degree is too small. Those RBFs and their corresponding minimum degrees are
‘multiquadric’ : 0
‘linear’ : 0
‘thin_plate_spline’ : 1
‘cubic’ : 1
‘quintic’ : 2
The default value is the minimum degree for kernel or 0 if there is no minimum degree. Set this to -1 for no added polynomial.
Notes
An RBF is a scalar valued function in N-dimensional space whose value at \(x\) can be expressed in terms of \(r=||x - c||\), where \(c\) is the center of the RBF.
An RBF interpolant for the vector of data values \(d\), which are from locations \(y\), is a linear combination of RBFs centered at \(y\) plus a polynomial with a specified degree. The RBF interpolant is written as
\[f(x) = K(x, y) a + P(x) b,\]where \(K(x, y)\) is a matrix of RBFs with centers at \(y\) evaluated at the points \(x\), and \(P(x)\) is a matrix of monomials, which span polynomials with the specified degree, evaluated at \(x\). The coefficients \(a\) and \(b\) are the solution to the linear equations
\[(K(y, y) + \lambda I) a + P(y) b = d\]and
\[P(y)^T a = 0,\]where \(\lambda\) is a non-negative smoothing parameter that controls how well we want to fit the data. The data are fit exactly when the smoothing parameter is 0.
The above system is uniquely solvable if the following requirements are met:
\(P(y)\) must have full column rank. \(P(y)\) always has full column rank when degree is -1 or 0. When degree is 1, \(P(y)\) has full column rank if the data point locations are not all collinear (N=2), coplanar (N=3), etc.
If kernel is ‘multiquadric’, ‘linear’, ‘thin_plate_spline’, ‘cubic’, or ‘quintic’, then degree must not be lower than the minimum value listed above.
If smoothing is 0, then each data point location must be distinct.
When using an RBF that is not scale invariant (‘multiquadric’, ‘inverse_multiquadric’, ‘inverse_quadratic’, or ‘gaussian’), an appropriate shape parameter must be chosen (e.g., through cross validation). Smaller values for the shape parameter correspond to wider RBFs. The problem can become ill-conditioned or singular when the shape parameter is too small.
The memory required to solve for the RBF interpolation coefficients increases quadratically with the number of data points, which can become impractical when interpolating more than about a thousand data points. To overcome memory limitations for large interpolation problems, the neighbors argument can be specified to compute an RBF interpolant for each evaluation point using only the nearest data points.
New in version 1.7.0.
References
- 1
Fasshauer, G., 2007. Meshfree Approximation Methods with Matlab. World Scientific Publishing Co.
- 2
- 3
Wahba, G., 1990. Spline Models for Observational Data. SIAM.
- 4
http://pages.stat.wisc.edu/~wahba/stat860public/lect/lect8/lect8.pdf
Examples
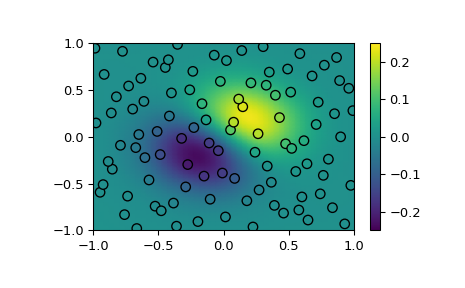
Demonstrate interpolating scattered data to a grid in 2-D.
>>> import matplotlib.pyplot as plt >>> from scipy.interpolate import RBFInterpolator >>> from scipy.stats.qmc import Halton
>>> rng = np.random.default_rng() >>> xobs = 2*Halton(2, seed=rng).random(100) - 1 >>> yobs = np.sum(xobs, axis=1)*np.exp(-6*np.sum(xobs**2, axis=1))
>>> xgrid = np.mgrid[-1:1:50j, -1:1:50j] >>> xflat = xgrid.reshape(2, -1).T >>> yflat = RBFInterpolator(xobs, yobs)(xflat) >>> ygrid = yflat.reshape(50, 50)
>>> fig, ax = plt.subplots() >>> ax.pcolormesh(*xgrid, ygrid, vmin=-0.25, vmax=0.25, shading='gouraud') >>> p = ax.scatter(*xobs.T, c=yobs, s=50, ec='k', vmin=-0.25, vmax=0.25) >>> fig.colorbar(p) >>> plt.show()
Methods
__call__(x)Evaluate the interpolant at x.