scipy.stats.boxcox_normmax

scipy.stats.boxcox_normmax(x, brack=- 2.0, 2.0, method='pearsonr')

Compute optimal Box-Cox transform parameter for input data.

Parameters

xarray_like

Input array.

brack2-tuple, optional

The starting interval for a downhill bracket search with optimize.brent. Note that this is in most cases not critical; the final result is allowed to be outside this bracket.

methodstr, optional

The method to determine the optimal transform parameter (boxcox lmbda parameter). Options are:

‘pearsonr’ (default)

Maximizes the Pearson correlation coefficient between y = boxcox(x) and the expected values for y if x would be normally-distributed.

‘mle’

Minimizes the log-likelihood boxcox_llf. This is the method used in boxcox.

‘all’

Use all optimization methods available, and return all results. Useful to compare different methods.

Returns

maxlogfloat or ndarray

The optimal transform parameter found. An array instead of a scalar for method='all'.

See also

boxcox, boxcox_llf, boxcox_normplot

Examples

>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> np.random.seed(1234)  # make this example reproducible

Generate some data and determine optimal lmbda in various ways:

>>> x = stats.loggamma.rvs(5, size=30) + 5
>>> y, lmax_mle = stats.boxcox(x)
>>> lmax_pearsonr = stats.boxcox_normmax(x)

>>> lmax_mle
7.177...
>>> lmax_pearsonr
7.916...
>>> stats.boxcox_normmax(x, method='all')
array([ 7.91667384,  7.17718692])

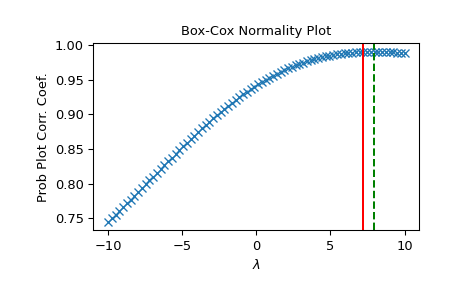
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> prob = stats.boxcox_normplot(x, -10, 10, plot=ax)
>>> ax.axvline(lmax_mle, color='r')
>>> ax.axvline(lmax_pearsonr, color='g', ls='--')

>>> plt.show()