Interpolation (scipy.interpolate)¶
Contents
There are several general interpolation facilities available in SciPy, for data in 1, 2, and higher dimensions:
A class representing an interpolant (
interp1d) in 1-D, offering several interpolation methods.Convenience function
griddataoffering a simple interface to interpolation in N dimensions (N = 1, 2, 3, 4, …). Object-oriented interface for the underlying routines is also available.Functions for 1- and 2-D (smoothed) cubic-spline interpolation, based on the FORTRAN library FITPACK. They are both procedural and object-oriented interfaces for the FITPACK library.
Interpolation using radial basis functions.
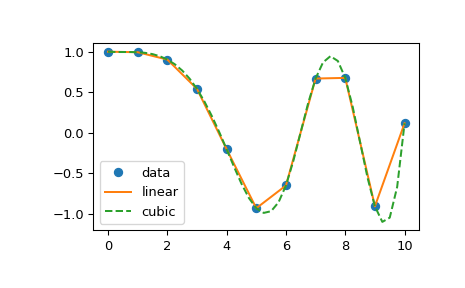
1-D interpolation (interp1d)¶
The interp1d class in scipy.interpolate is a convenient method to
create a function based on fixed data points, which can be evaluated
anywhere within the domain defined by the given data using linear
interpolation. An instance of this class is created by passing the 1-D
vectors comprising the data. The instance of this class defines a
__call__ method and can therefore by treated like a function which
interpolates between known data values to obtain unknown values (it
also has a docstring for help). Behavior at the boundary can be
specified at instantiation time. The following example demonstrates
its use, for linear and cubic spline interpolation:
>>> from scipy.interpolate import interp1d
>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f = interp1d(x, y)
>>> f2 = interp1d(x, y, kind='cubic')
>>> xnew = np.linspace(0, 10, num=41, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
>>> plt.legend(['data', 'linear', 'cubic'], loc='best')
>>> plt.show()
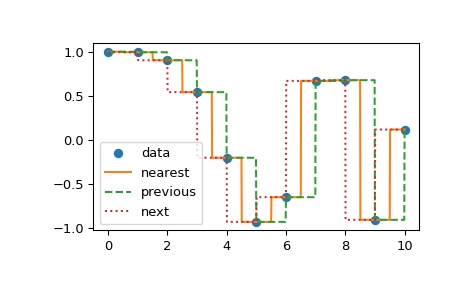
Another set of interpolations in interp1d is nearest, previous, and
next, where they return the nearest, previous, or next point along the
x-axis. Nearest and next can be thought of as a special case of a causal
interpolating filter. The following example demonstrates their use, using the
same data as in the previous example:
>>> from scipy.interpolate import interp1d
>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f1 = interp1d(x, y, kind='nearest')
>>> f2 = interp1d(x, y, kind='previous')
>>> f3 = interp1d(x, y, kind='next')
>>> xnew = np.linspace(0, 10, num=1001, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
>>> plt.plot(xnew, f1(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), ':')
>>> plt.legend(['data', 'nearest', 'previous', 'next'], loc='best')
>>> plt.show()
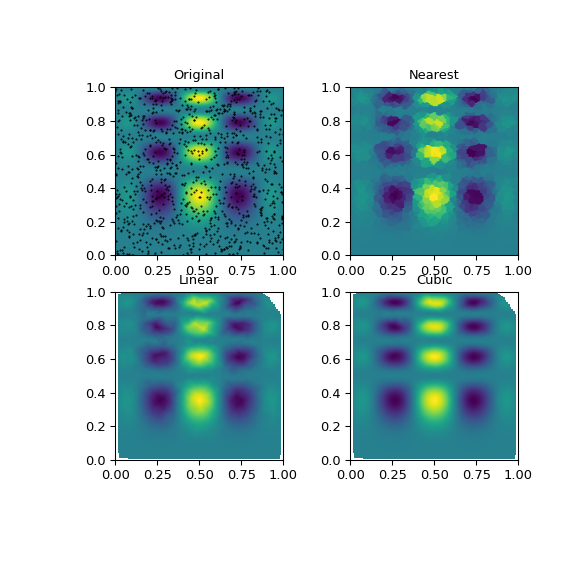
Multivariate data interpolation (griddata)¶
Suppose you have multidimensional data, for instance, for an underlying function f(x, y) you only know the values at points (x[i], y[i]) that do not form a regular grid.
Suppose we want to interpolate the 2-D function
>>> def func(x, y):
... return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
on a grid in [0, 1]x[0, 1]
>>> grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]
but we only know its values at 1000 data points:
>>> points = np.random.rand(1000, 2)
>>> values = func(points[:,0], points[:,1])
This can be done with griddata – below, we try out all of the
interpolation methods:
>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')
One can see that the exact result is reproduced by all of the methods to some degree, but for this smooth function the piecewise cubic interpolant gives the best results:
>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
>>> plt.plot(points[:,0], points[:,1], 'k.', ms=1)
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()
Spline interpolation¶
Spline interpolation in 1-D: Procedural (interpolate.splXXX)¶
Spline interpolation requires two essential steps: (1) a spline
representation of the curve is computed, and (2) the spline is
evaluated at the desired points. In order to find the spline
representation, there are two different ways to represent a curve and
obtain (smoothing) spline coefficients: directly and parametrically.
The direct method finds the spline representation of a curve in a 2-D
plane using the function splrep. The
first two arguments are the only ones required, and these provide the
\(x\) and \(y\) components of the curve. The normal output is
a 3-tuple, \(\left(t,c,k\right)\) , containing the knot-points,
\(t\) , the coefficients \(c\) and the order \(k\) of the
spline. The default spline order is cubic, but this can be changed
with the input keyword, k.
For curves in N-D space the function
splprep allows defining the curve
parametrically. For this function only 1 input argument is
required. This input is a list of \(N\)-arrays representing the
curve in N-D space. The length of each array is the
number of curve points, and each array provides one component of the
N-D data point. The parameter variable is given
with the keyword argument, u,, which defaults to an equally-spaced
monotonic sequence between \(0\) and \(1\) . The default
output consists of two objects: a 3-tuple, \(\left(t,c,k\right)\)
, containing the spline representation and the parameter variable
\(u.\)
The keyword argument, s , is used to specify the amount of smoothing to perform during the spline fit. The default value of \(s\) is \(s=m-\sqrt{2m}\) where \(m\) is the number of data-points being fit. Therefore, if no smoothing is desired a value of \(\mathbf{s}=0\) should be passed to the routines.
Once the spline representation of the data has been determined,
functions are available for evaluating the spline
(splev) and its derivatives
(splev, spalde) at any point
and the integral of the spline between any two points (
splint). In addition, for cubic splines ( \(k=3\)
) with 8 or more knots, the roots of the spline can be estimated (
sproot). These functions are demonstrated in the
example that follows.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
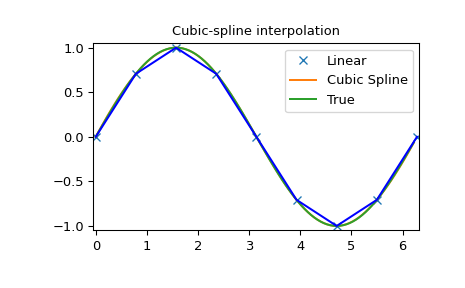
Cubic-spline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = interpolate.splev(xnew, tck, der=0)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Cubic-spline interpolation')
>>> plt.show()
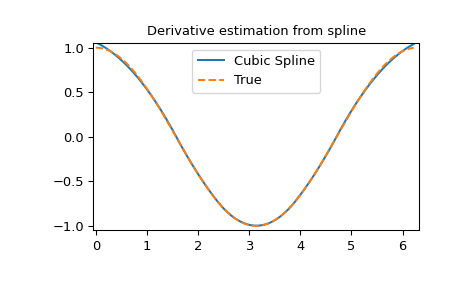
Derivative of spline
>>> yder = interpolate.splev(xnew, tck, der=1)
>>> plt.figure()
>>> plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Derivative estimation from spline')
>>> plt.show()
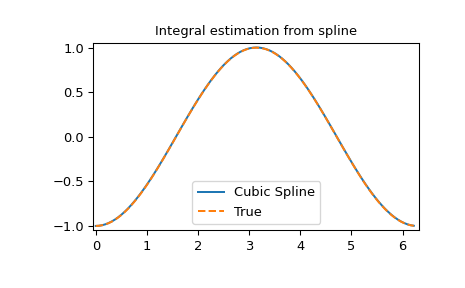
Integral of spline
>>> def integ(x, tck, constant=-1):
... x = np.atleast_1d(x)
... out = np.zeros(x.shape, dtype=x.dtype)
... for n in range(len(out)):
... out[n] = interpolate.splint(0, x[n], tck)
... out += constant
... return out
>>> yint = integ(xnew, tck)
>>> plt.figure()
>>> plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Integral estimation from spline')
>>> plt.show()
Roots of spline
>>> interpolate.sproot(tck)
array([3.1416])
Notice that sproot failed to find an obvious solution at the edge of the
approximation interval, \(x = 0\). If we define the spline on a slightly
larger interval, we recover both roots \(x = 0\) and \(x = 2\pi\):
>>> x = np.linspace(-np.pi/4, 2.*np.pi + np.pi/4, 21)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> interpolate.sproot(tck)
array([0., 3.1416])
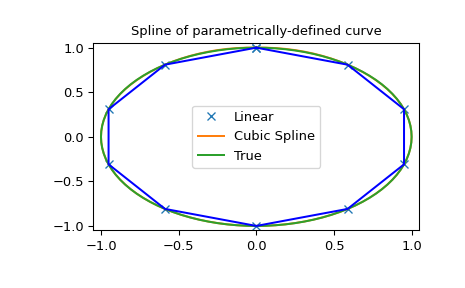
Parametric spline
>>> t = np.arange(0, 1.1, .1)
>>> x = np.sin(2*np.pi*t)
>>> y = np.cos(2*np.pi*t)
>>> tck, u = interpolate.splprep([x, y], s=0)
>>> unew = np.arange(0, 1.01, 0.01)
>>> out = interpolate.splev(unew, tck)
>>> plt.figure()
>>> plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-1.05, 1.05, -1.05, 1.05])
>>> plt.title('Spline of parametrically-defined curve')
>>> plt.show()
Spline interpolation in 1-d: Object-oriented (UnivariateSpline)¶
The spline-fitting capabilities described above are also available via
an objected-oriented interface. The 1-D splines are
objects of the UnivariateSpline class, and are created with the
\(x\) and \(y\) components of the curve provided as arguments
to the constructor. The class defines __call__, allowing the object
to be called with the x-axis values, at which the spline should be
evaluated, returning the interpolated y-values. This is shown in
the example below for the subclass InterpolatedUnivariateSpline.
The integral,
derivatives, and
roots methods are also available
on UnivariateSpline objects, allowing definite integrals,
derivatives, and roots to be computed for the spline.
The UnivariateSpline class can also be used to smooth data by
providing a non-zero value of the smoothing parameter s, with the
same meaning as the s keyword of the splrep function
described above. This results in a spline that has fewer knots
than the number of data points, and hence is no longer strictly
an interpolating spline, but rather a smoothing spline. If this
is not desired, the InterpolatedUnivariateSpline class is available.
It is a subclass of UnivariateSpline that always passes through all
points (equivalent to forcing the smoothing parameter to 0). This
class is demonstrated in the example below.
The LSQUnivariateSpline class is the other subclass of UnivariateSpline.
It allows the user to specify the number and location of internal
knots explicitly with the parameter t. This allows for the creation
of customized splines with non-linear spacing, to interpolate in
some domains and smooth in others, or change the character of the
spline.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
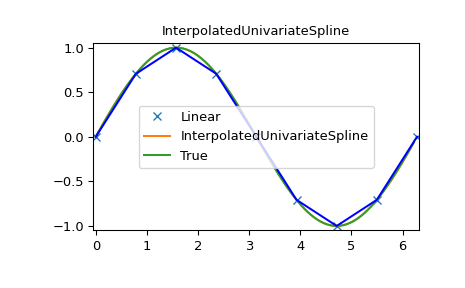
InterpolatedUnivariateSpline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> s = interpolate.InterpolatedUnivariateSpline(x, y)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('InterpolatedUnivariateSpline')
>>> plt.show()
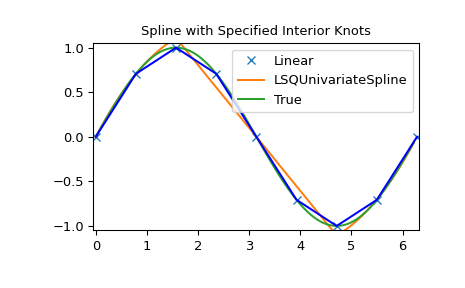
LSQUnivarateSpline with non-uniform knots
>>> t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
>>> s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Spline with Specified Interior Knots')
>>> plt.show()
2-D spline representation: Procedural (bisplrep)¶
For (smooth) spline-fitting to a 2-D surface, the function
bisplrep is available. This function takes as required inputs
the 1-D arrays x, y, and z, which represent points on the
surface \(z=f\left(x,y\right).\) The default output is a list
\(\left[tx,ty,c,kx,ky\right]\) whose entries represent
respectively, the components of the knot positions, the coefficients
of the spline, and the order of the spline in each coordinate. It is
convenient to hold this list in a single object, tck, so that it can
be passed easily to the function bisplev. The
keyword, s , can be used to change the amount of smoothing performed
on the data while determining the appropriate spline. The default
value is \(s=m-\sqrt{2m}\), where \(m\) is the number of data
points in the x, y, and z vectors. As a result, if no smoothing is
desired, then \(s=0\) should be passed to
bisplrep.
To evaluate the 2-D spline and its partial derivatives
(up to the order of the spline), the function
bisplev is required. This function takes as the
first two arguments two 1-D arrays whose cross-product specifies
the domain over which to evaluate the spline. The third argument is
the tck list returned from bisplrep. If desired,
the fourth and fifth arguments provide the orders of the partial
derivative in the \(x\) and \(y\) direction, respectively.
It is important to note that 2-D interpolation should not
be used to find the spline representation of images. The algorithm
used is not amenable to large numbers of input points. The signal-processing
toolbox contains more appropriate algorithms for finding
the spline representation of an image. The 2-D
interpolation commands are intended for use when interpolating a 2-D
function as shown in the example that follows. This
example uses the mgrid command in NumPy which is
useful for defining a “mesh-grid” in many dimensions. (See also the
ogrid command if the full-mesh is not
needed). The number of output arguments and the number of dimensions
of each argument is determined by the number of indexing objects
passed in mgrid.
>>> import numpy as np
>>> from scipy import interpolate
>>> import matplotlib.pyplot as plt
Define function over a sparse 20x20 grid
>>> x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
>>> x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
>>> y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
>>> z = (x+y) * np.exp(-6.0*(x*x+y*y))
>>> plt.figure()
>>> lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
>>> plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Sparsely sampled function.")
>>> plt.show()
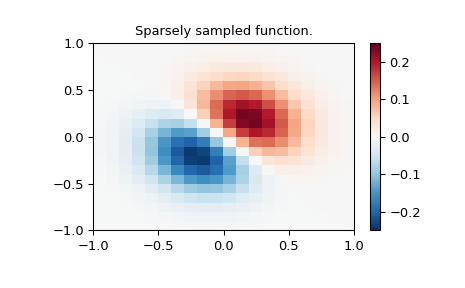
Interpolate function over a new 70x70 grid
>>> xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
>>> xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
>>> ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
>>> tck = interpolate.bisplrep(x, y, z, s=0)
>>> znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)
>>> plt.figure()
>>> plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Interpolated function.")
>>> plt.show()
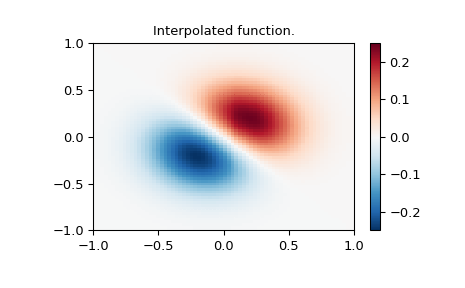
2-D spline representation: Object-oriented (BivariateSpline)¶
The BivariateSpline class is the 2-D analog of the
UnivariateSpline class. It and its subclasses implement
the FITPACK functions described above in an object-oriented fashion,
allowing objects to be instantiated that can be called to compute
the spline value by passing in the two coordinates as the two
arguments.
Using radial basis functions for smoothing/interpolation¶
Radial basis functions can be used for smoothing/interpolating scattered data in N dimensions, but should be used with caution for extrapolation outside of the observed data range.
1-D Example¶
This example compares the usage of the Rbf and UnivariateSpline classes
from the scipy.interpolate module.
>>> import numpy as np
>>> from scipy.interpolate import Rbf, InterpolatedUnivariateSpline
>>> import matplotlib.pyplot as plt
>>> # setup data
>>> x = np.linspace(0, 10, 9)
>>> y = np.sin(x)
>>> xi = np.linspace(0, 10, 101)
>>> # use fitpack2 method
>>> ius = InterpolatedUnivariateSpline(x, y)
>>> yi = ius(xi)
>>> plt.subplot(2, 1, 1)
>>> plt.plot(x, y, 'bo')
>>> plt.plot(xi, yi, 'g')
>>> plt.plot(xi, np.sin(xi), 'r')
>>> plt.title('Interpolation using univariate spline')
>>> # use RBF method
>>> rbf = Rbf(x, y)
>>> fi = rbf(xi)
>>> plt.subplot(2, 1, 2)
>>> plt.plot(x, y, 'bo')
>>> plt.plot(xi, fi, 'g')
>>> plt.plot(xi, np.sin(xi), 'r')
>>> plt.title('Interpolation using RBF - multiquadrics')
>>> plt.show()
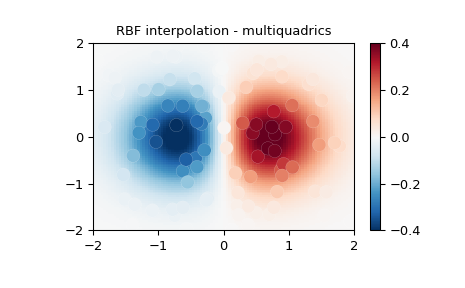
2-D Example¶
This example shows how to interpolate scattered 2-D data:
>>> import numpy as np
>>> from scipy.interpolate import Rbf
>>> import matplotlib.pyplot as plt
>>> from matplotlib import cm
>>> # 2-d tests - setup scattered data
>>> x = np.random.rand(100)*4.0-2.0
>>> y = np.random.rand(100)*4.0-2.0
>>> z = x*np.exp(-x**2-y**2)
>>> edges = np.linspace(-2.0, 2.0, 101)
>>> centers = edges[:-1] + np.diff(edges[:2])[0] / 2.
>>> XI, YI = np.meshgrid(centers, centers)
>>> # use RBF
>>> rbf = Rbf(x, y, z, epsilon=2)
>>> ZI = rbf(XI, YI)
>>> # plot the result
>>> plt.subplot(1, 1, 1)
>>> X_edges, Y_edges = np.meshgrid(edges, edges)
>>> lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
>>> plt.pcolormesh(X_edges, Y_edges, ZI, shading='flat', **lims)
>>> plt.scatter(x, y, 100, z, edgecolor='w', lw=0.1, **lims)
>>> plt.title('RBF interpolation - multiquadrics')
>>> plt.xlim(-2, 2)
>>> plt.ylim(-2, 2)
>>> plt.colorbar()