scipy.special.kolmogorov

scipy.special.kolmogorov(y) = <ufunc 'kolmogorov'>

Complementary cumulative distribution (Survival Function) function of Kolmogorov distribution.

Returns the complementary cumulative distribution function of Kolmogorov’s limiting distribution (D_n*\sqrt(n) as n goes to infinity) of a two-sided test for equality between an empirical and a theoretical distribution. It is equal to the (limit as n->infinity of the) probability that sqrt(n) * max absolute deviation > y.

Parameters

yfloat array_like

Absolute deviation between the Empirical CDF (ECDF) and the target CDF, multiplied by sqrt(n).

Returns

float

The value(s) of kolmogorov(y)

See also

kolmogi

The Inverse Survival Function for the distribution

scipy.stats.kstwobign

Provides the functionality as a continuous distribution

smirnov, smirnovi

Functions for the one-sided distribution

Notes

kolmogorov is used by stats.kstest in the application of the Kolmogorov-Smirnov Goodness of Fit test. For historial reasons this function is exposed in scpy.special, but the recommended way to achieve the most accurate CDF/SF/PDF/PPF/ISF computations is to use the stats.kstwobign distribution.

Examples

Show the probability of a gap at least as big as 0, 0.5 and 1.0.

>>> from scipy.special import kolmogorov
>>> from scipy.stats import kstwobign
>>> kolmogorov([0, 0.5, 1.0])
array([ 1.        ,  0.96394524,  0.26999967])

Compare a sample of size 1000 drawn from a Laplace(0, 1) distribution against the target distribution, a Normal(0, 1) distribution.

>>> from scipy.stats import norm, laplace
>>> n = 1000
>>> np.random.seed(seed=233423)
>>> lap01 = laplace(0, 1)
>>> x = np.sort(lap01.rvs(n))
>>> np.mean(x), np.std(x)
(-0.083073685397609842, 1.3676426568399822)

Construct the Empirical CDF and the K-S statistic Dn.

>>> target = norm(0,1)  # Normal mean 0, stddev 1
>>> cdfs = target.cdf(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> gaps = np.column_stack([cdfs - ecdfs[:n], ecdfs[1:] - cdfs])
>>> Dn = np.max(gaps)
>>> Kn = np.sqrt(n) * Dn
>>> print('Dn=%f, sqrt(n)*Dn=%f' % (Dn, Kn))
Dn=0.058286, sqrt(n)*Dn=1.843153
>>> print(chr(10).join(['For a sample of size n drawn from a N(0, 1) distribution:',
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn>=%f is %f' %  (Kn, kolmogorov(Kn)),
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn<=%f is %f' %  (Kn, kstwobign.cdf(Kn))]))
For a sample of size n drawn from a N(0, 1) distribution:
 the approximate Kolmogorov probability that sqrt(n)*Dn>=1.843153 is 0.002240
 the approximate Kolmogorov probability that sqrt(n)*Dn<=1.843153 is 0.997760

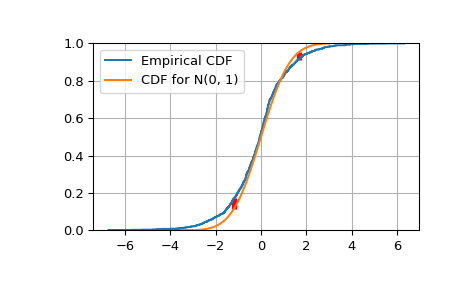
Plot the Empirical CDF against the target N(0, 1) CDF.

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate([[-3], x]), ecdfs, where='post', label='Empirical CDF')
>>> x3 = np.linspace(-3, 3, 100)
>>> plt.plot(x3, target.cdf(x3), label='CDF for N(0, 1)')
>>> plt.ylim([0, 1]); plt.grid(True); plt.legend();
>>> # Add vertical lines marking Dn+ and Dn-
>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus], color='r', linestyle='dashed', lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1], color='r', linestyle='dashed', lw=4)
>>> plt.show()