scipy.signal.windows.tukey

scipy.signal.windows.tukey(M, alpha=0.5, sym=True)

Return a Tukey window, also known as a tapered cosine window.

Parameters

Mint

Number of points in the output window. If zero or less, an empty array is returned.

alphafloat, optional

Shape parameter of the Tukey window, representing the fraction of the window inside the cosine tapered region. If zero, the Tukey window is equivalent to a rectangular window. If one, the Tukey window is equivalent to a Hann window.

symbool, optional

When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.

Returns

wndarray

The window, with the maximum value normalized to 1 (though the value 1 does not appear if M is even and sym is True).

References

1

Harris, Fredric J. (Jan 1978). “On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform”. Proceedings of the IEEE 66 (1): 51-83. DOI:10.1109/PROC.1978.10837

2

Wikipedia, “Window function”, https://en.wikipedia.org/wiki/Window_function#Tukey_window

Examples

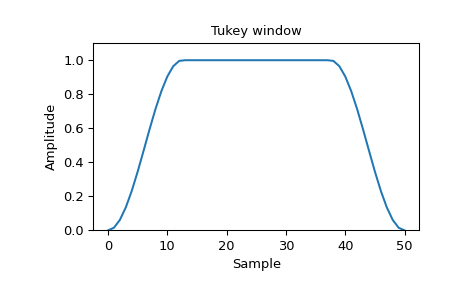
Plot the window and its frequency response:

>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.tukey(51)
>>> plt.plot(window)
>>> plt.title("Tukey window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")
>>> plt.ylim([0, 1.1])

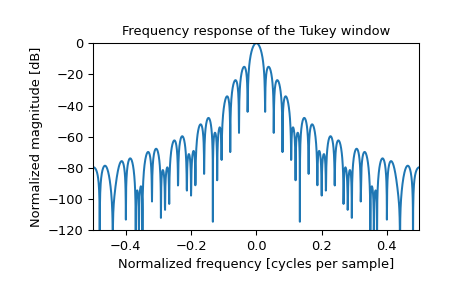
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Tukey window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")