scipy.signal.ellipord

scipy.signal.ellipord(wp, ws, gpass, gstop, analog=False, fs=None)

Elliptic (Cauer) filter order selection.

Return the order of the lowest order digital or analog elliptic filter that loses no more than gpass dB in the passband and has at least gstop dB attenuation in the stopband.

Parameters

wp, wsfloat

Passband and stopband edge frequencies.

For digital filters, these are in the same units as fs. By default, fs is 2 half-cycles/sample, so these are normalized from 0 to 1, where 1 is the Nyquist frequency. (wp and ws are thus in half-cycles / sample.) For example:

• Lowpass: wp = 0.2, ws = 0.3

• Highpass: wp = 0.3, ws = 0.2

• Bandpass: wp = [0.2, 0.5], ws = [0.1, 0.6]

• Bandstop: wp = [0.1, 0.6], ws = [0.2, 0.5]

For analog filters, wp and ws are angular frequencies (e.g., rad/s).

gpassfloat

The maximum loss in the passband (dB).

gstopfloat

The minimum attenuation in the stopband (dB).

analogbool, optional

When True, return an analog filter, otherwise a digital filter is returned.

fsfloat, optional

The sampling frequency of the digital system.

New in version 1.2.0.

Returns

ordint

The lowest order for an Elliptic (Cauer) filter that meets specs.

wnndarray or float

The Chebyshev natural frequency (the “3dB frequency”) for use with ellip to give filter results. If fs is specified, this is in the same units, and fs must also be passed to ellip.

See also

ellip

Filter design using order and critical points

buttord

Find order and critical points from passband and stopband spec

cheb1ord, cheb2ord

iirfilter

General filter design using order and critical frequencies

iirdesign

General filter design using passband and stopband spec

Examples

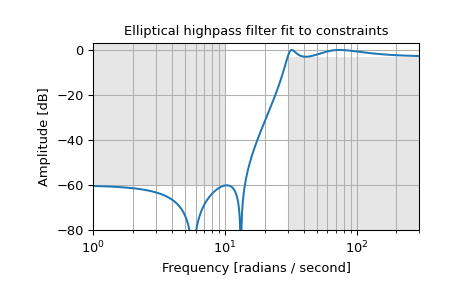
Design an analog highpass filter such that the passband is within 3 dB above 30 rad/s, while rejecting -60 dB at 10 rad/s. Plot its frequency response, showing the passband and stopband constraints in gray.

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> N, Wn = signal.ellipord(30, 10, 3, 60, True)
>>> b, a = signal.ellip(N, 3, 60, Wn, 'high', True)
>>> w, h = signal.freqs(b, a, np.logspace(0, 3, 500))
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Elliptical highpass filter fit to constraints')
>>> plt.xlabel('Frequency [radians / second]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(which='both', axis='both')
>>> plt.fill([.1, 10,  10,  .1], [1e4, 1e4, -60, -60], '0.9', lw=0) # stop
>>> plt.fill([30, 30, 1e9, 1e9], [-99,  -3,  -3, -99], '0.9', lw=0) # pass
>>> plt.axis([1, 300, -80, 3])
>>> plt.show()