scipy.cluster.vq.kmeans

scipy.cluster.vq.kmeans(obs, k_or_guess, iter=20, thresh=1e-05, check_finite=True)

Performs k-means on a set of observation vectors forming k clusters.

The k-means algorithm adjusts the classification of the observations into clusters and updates the cluster centroids until the position of the centroids is stable over successive iterations. In this implementation of the algorithm, the stability of the centroids is determined by comparing the absolute value of the change in the average Euclidean distance between the observations and their corresponding centroids against a threshold. This yields a code book mapping centroids to codes and vice versa.

Parameters

obsndarray

Each row of the M by N array is an observation vector. The columns are the features seen during each observation. The features must be whitened first with the whiten function.

k_or_guessint or ndarray

The number of centroids to generate. A code is assigned to each centroid, which is also the row index of the centroid in the code_book matrix generated.

The initial k centroids are chosen by randomly selecting observations from the observation matrix. Alternatively, passing a k by N array specifies the initial k centroids.

iterint, optional

The number of times to run k-means, returning the codebook with the lowest distortion. This argument is ignored if initial centroids are specified with an array for the k_or_guess parameter. This parameter does not represent the number of iterations of the k-means algorithm.

threshfloat, optional

Terminates the k-means algorithm if the change in distortion since the last k-means iteration is less than or equal to threshold.

check_finitebool, optional

Whether to check that the input matrices contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs. Default: True

Returns

codebookndarray

A k by N array of k centroids. The ith centroid codebook[i] is represented with the code i. The centroids and codes generated represent the lowest distortion seen, not necessarily the globally minimal distortion.

distortionfloat

The mean (non-squared) Euclidean distance between the observations passed and the centroids generated. Note the difference to the standard definition of distortion in the context of the k-means algorithm, which is the sum of the squared distances.

See also

kmeans2

a different implementation of k-means clustering with more methods for generating initial centroids but without using a distortion change threshold as a stopping criterion.

whiten

must be called prior to passing an observation matrix to kmeans.

Examples

>>> from numpy import array
>>> from scipy.cluster.vq import vq, kmeans, whiten
>>> import matplotlib.pyplot as plt
>>> features  = array([[ 1.9,2.3],
...                    [ 1.5,2.5],
...                    [ 0.8,0.6],
...                    [ 0.4,1.8],
...                    [ 0.1,0.1],
...                    [ 0.2,1.8],
...                    [ 2.0,0.5],
...                    [ 0.3,1.5],
...                    [ 1.0,1.0]])
>>> whitened = whiten(features)
>>> book = np.array((whitened[0],whitened[2]))
>>> kmeans(whitened,book)
(array([[ 2.3110306 ,  2.86287398],    # random
       [ 0.93218041,  1.24398691]]), 0.85684700941625547)

>>> from numpy import random
>>> random.seed((1000,2000))
>>> codes = 3
>>> kmeans(whitened,codes)
(array([[ 2.3110306 ,  2.86287398],    # random
       [ 1.32544402,  0.65607529],
       [ 0.40782893,  2.02786907]]), 0.5196582527686241)

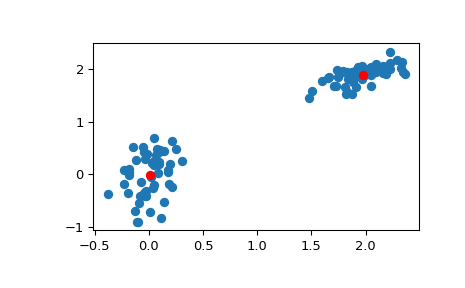
>>> # Create 50 datapoints in two clusters a and b
>>> pts = 50
>>> a = np.random.multivariate_normal([0, 0], [[4, 1], [1, 4]], size=pts)
>>> b = np.random.multivariate_normal([30, 10],
...                                   [[10, 2], [2, 1]],
...                                   size=pts)
>>> features = np.concatenate((a, b))
>>> # Whiten data
>>> whitened = whiten(features)
>>> # Find 2 clusters in the data
>>> codebook, distortion = kmeans(whitened, 2)
>>> # Plot whitened data and cluster centers in red
>>> plt.scatter(whitened[:, 0], whitened[:, 1])
>>> plt.scatter(codebook[:, 0], codebook[:, 1], c='r')
>>> plt.show()