scipy.spatial.SphericalVoronoi

class scipy.spatial.SphericalVoronoi(points, radius=1, center=None, threshold=1e-06)

Voronoi diagrams on the surface of a sphere.

New in version 0.18.0.

Parameters

pointsndarray of floats, shape (npoints, ndim)

Coordinates of points from which to construct a spherical Voronoi diagram.

radiusfloat, optional

Radius of the sphere (Default: 1)

centerndarray of floats, shape (ndim,)

Center of sphere (Default: origin)

thresholdfloat

Threshold for detecting duplicate points and mismatches between points and sphere parameters. (Default: 1e-06)

Raises

ValueError

If there are duplicates in points. If the provided radius is not consistent with points.

See also

Voronoi

Conventional Voronoi diagrams in N dimensions.

Notes

The spherical Voronoi diagram algorithm proceeds as follows. The Convex Hull of the input points (generators) is calculated, and is equivalent to their Delaunay triangulation on the surface of the sphere [R9133a064969a-Caroli]. The Convex Hull neighbour information is then used to order the Voronoi region vertices around each generator. The latter approach is substantially less sensitive to floating point issues than angle-based methods of Voronoi region vertex sorting.

Empirical assessment of spherical Voronoi algorithm performance suggests quadratic time complexity (loglinear is optimal, but algorithms are more challenging to implement).

References

R9133a064969a-Caroli

Caroli et al. Robust and Efficient Delaunay triangulations of points on or close to a sphere. Research Report RR-7004, 2009.

Examples

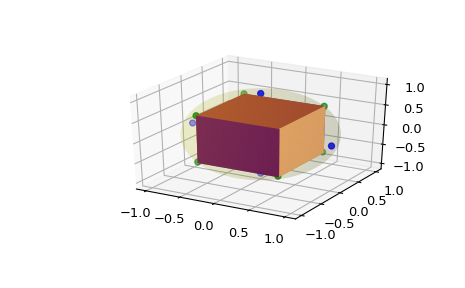
Do some imports and take some points on a cube:

>>> from matplotlib import colors
>>> from mpl_toolkits.mplot3d.art3d import Poly3DCollection
>>> import matplotlib.pyplot as plt
>>> from scipy.spatial import SphericalVoronoi
>>> from mpl_toolkits.mplot3d import proj3d
>>> # set input data
>>> points = np.array([[0, 0, 1], [0, 0, -1], [1, 0, 0],
...                    [0, 1, 0], [0, -1, 0], [-1, 0, 0], ])

Calculate the spherical Voronoi diagram:

>>> radius = 1
>>> center = np.array([0, 0, 0])
>>> sv = SphericalVoronoi(points, radius, center)

Generate plot:

>>> # sort vertices (optional, helpful for plotting)
>>> sv.sort_vertices_of_regions()
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> # plot the unit sphere for reference (optional)
>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)
>>> # plot generator points
>>> ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='b')
>>> # plot Voronoi vertices
>>> ax.scatter(sv.vertices[:, 0], sv.vertices[:, 1], sv.vertices[:, 2],
...                    c='g')
>>> # indicate Voronoi regions (as Euclidean polygons)
>>> for region in sv.regions:
...    random_color = colors.rgb2hex(np.random.rand(3))
...    polygon = Poly3DCollection([sv.vertices[region]], alpha=1.0)
...    polygon.set_color(random_color)
...    ax.add_collection3d(polygon)
>>> plt.show()

Attributes

pointsdouble array of shape (npoints, ndim)

the points in ndim dimensions to generate the Voronoi diagram from

radiusdouble

radius of the sphere

centerdouble array of shape (ndim,)

center of the sphere

verticesdouble array of shape (nvertices, ndim)

Voronoi vertices corresponding to points

regionslist of list of integers of shape (npoints, _ )

the n-th entry is a list consisting of the indices of the vertices belonging to the n-th point in points

Methods

sort_vertices_of_regions(self)

Sort indices of the vertices to be (counter-)clockwise ordered.