scipy.signal.freqs_zpk

scipy.signal.freqs_zpk(z, p, k, worN=200)

Compute frequency response of analog filter.

Given the zeros z, poles p, and gain k of a filter, compute its frequency response:

           (jw-z[0]) * (jw-z[1]) * ... * (jw-z[-1])
H(w) = k * ----------------------------------------
           (jw-p[0]) * (jw-p[1]) * ... * (jw-p[-1])

Parameters

zarray_like

Zeroes of a linear filter

parray_like

Poles of a linear filter

kscalar

Gain of a linear filter

worN{None, int, array_like}, optional

If None, then compute at 200 frequencies around the interesting parts of the response curve (determined by pole-zero locations). If a single integer, then compute at that many frequencies. Otherwise, compute the response at the angular frequencies (e.g. rad/s) given in worN.

Returns

wndarray

The angular frequencies at which h was computed.

hndarray

The frequency response.

See also

freqs

Compute the frequency response of an analog filter in TF form

freqz

Compute the frequency response of a digital filter in TF form

freqz_zpk

Compute the frequency response of a digital filter in ZPK form

Notes

New in version 0.19.0.

Examples

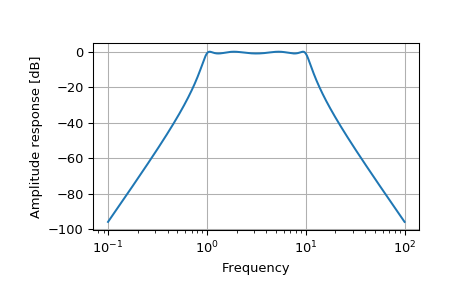
>>> from scipy.signal import freqs_zpk, iirfilter

>>> z, p, k = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1',
...                     output='zpk')

>>> w, h = freqs_zpk(z, p, k, worN=np.logspace(-1, 2, 1000))

>>> import matplotlib.pyplot as plt
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.xlabel('Frequency')
>>> plt.ylabel('Amplitude response [dB]')
>>> plt.grid()
>>> plt.show()