scipy.interpolate.BSpline.basis_element¶
-
classmethod
BSpline.basis_element(t, extrapolate=True)[source]¶ Return a B-spline basis element
B(x | t[0], ..., t[k+1]).- Parameters
- tndarray, shape (k+1,)
internal knots
- extrapolatebool or ‘periodic’, optional
whether to extrapolate beyond the base interval,
t[0] .. t[k+1], or to return nans. If ‘periodic’, periodic extrapolation is used. Default is True.
- Returns
- basis_elementcallable
A callable representing a B-spline basis element for the knot vector t.
Notes
The order of the b-spline, k, is inferred from the length of t as
len(t)-2. The knot vector is constructed by appending and prependingk+1elements to internal knots t.Examples
Construct a cubic b-spline:
>>> from scipy.interpolate import BSpline >>> b = BSpline.basis_element([0, 1, 2, 3, 4]) >>> k = b.k >>> b.t[k:-k] array([ 0., 1., 2., 3., 4.]) >>> k 3
Construct a second order b-spline on
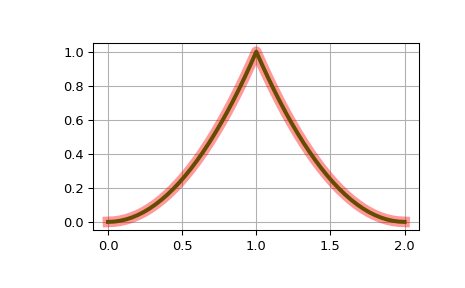
[0, 1, 1, 2], and compare to its explicit form:>>> t = [-1, 0, 1, 1, 2] >>> b = BSpline.basis_element(t[1:]) >>> def f(x): ... return np.where(x < 1, x*x, (2. - x)**2)
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> x = np.linspace(0, 2, 51) >>> ax.plot(x, b(x), 'g', lw=3) >>> ax.plot(x, f(x), 'r', lw=8, alpha=0.4) >>> ax.grid(True) >>> plt.show()