scipy.signal.hilbert

scipy.signal.hilbert(x, N=None, axis=-1)

Compute the analytic signal, using the Hilbert transform.

The transformation is done along the last axis by default.

Parameters

xarray_like

Signal data. Must be real.

Nint, optional

Number of Fourier components. Default: x.shape[axis]

axisint, optional

Axis along which to do the transformation. Default: -1.

Returns

xandarray

Analytic signal of x, of each 1-D array along axis

See also

scipy.fftpack.hilbert

Return Hilbert transform of a periodic sequence x.

Notes

The analytic signal x_a(t) of signal x(t) is:

\[x_a = F^{-1}(F(x) 2U) = x + i y\]

where F is the Fourier transform, U the unit step function, and y the Hilbert transform of x. [1]

In other words, the negative half of the frequency spectrum is zeroed out, turning the real-valued signal into a complex signal. The Hilbert transformed signal can be obtained from np.imag(hilbert(x)), and the original signal from np.real(hilbert(x)).

References

1

Wikipedia, “Analytic signal”. https://en.wikipedia.org/wiki/Analytic_signal

2

Leon Cohen, “Time-Frequency Analysis”, 1995. Chapter 2.

3

Alan V. Oppenheim, Ronald W. Schafer. Discrete-Time Signal Processing, Third Edition, 2009. Chapter 12. ISBN 13: 978-1292-02572-8

Examples

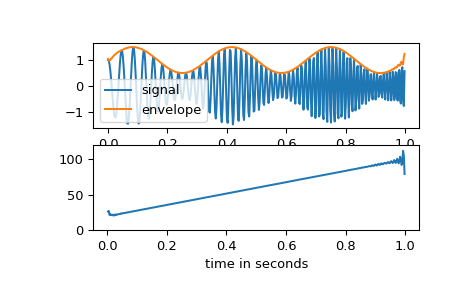
In this example we use the Hilbert transform to determine the amplitude envelope and instantaneous frequency of an amplitude-modulated signal.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import hilbert, chirp

>>> duration = 1.0
>>> fs = 400.0
>>> samples = int(fs*duration)
>>> t = np.arange(samples) / fs

We create a chirp of which the frequency increases from 20 Hz to 100 Hz and apply an amplitude modulation.

>>> signal = chirp(t, 20.0, t[-1], 100.0)
>>> signal *= (1.0 + 0.5 * np.sin(2.0*np.pi*3.0*t) )

The amplitude envelope is given by magnitude of the analytic signal. The instantaneous frequency can be obtained by differentiating the instantaneous phase in respect to time. The instantaneous phase corresponds to the phase angle of the analytic signal.

>>> analytic_signal = hilbert(signal)
>>> amplitude_envelope = np.abs(analytic_signal)
>>> instantaneous_phase = np.unwrap(np.angle(analytic_signal))
>>> instantaneous_frequency = (np.diff(instantaneous_phase) /
...                            (2.0*np.pi) * fs)

>>> fig = plt.figure()
>>> ax0 = fig.add_subplot(211)
>>> ax0.plot(t, signal, label='signal')
>>> ax0.plot(t, amplitude_envelope, label='envelope')
>>> ax0.set_xlabel("time in seconds")
>>> ax0.legend()
>>> ax1 = fig.add_subplot(212)
>>> ax1.plot(t[1:], instantaneous_frequency)
>>> ax1.set_xlabel("time in seconds")
>>> ax1.set_ylim(0.0, 120.0)