scipy.signal.cheby1

scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba', fs=None)

Chebyshev type I digital and analog filter design.

Design an Nth-order digital or analog Chebyshev type I filter and return the filter coefficients.

Parameters

Nint

The order of the filter.

rpfloat

The maximum ripple allowed below unity gain in the passband. Specified in decibels, as a positive number.

Wnarray_like

A scalar or length-2 sequence giving the critical frequencies. For Type I filters, this is the point in the transition band at which the gain first drops below -rp.

For digital filters, Wn are in the same units as fs. By default, fs is 2 half-cycles/sample, so these are normalized from 0 to 1, where 1 is the Nyquist frequency. (Wn is thus in half-cycles / sample.)

For analog filters, Wn is an angular frequency (e.g. rad/s).

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional

The type of filter. Default is ‘lowpass’.

analogbool, optional

When True, return an analog filter, otherwise a digital filter is returned.

output{‘ba’, ‘zpk’, ‘sos’}, optional

Type of output: numerator/denominator (‘ba’), pole-zero (‘zpk’), or second-order sections (‘sos’). Default is ‘ba’.

fsfloat, optional

The sampling frequency of the digital system.

New in version 1.2.0.

Returns

b, andarray, ndarray

Numerator (b) and denominator (a) polynomials of the IIR filter. Only returned if output='ba'.

z, p, kndarray, ndarray, float

Zeros, poles, and system gain of the IIR filter transfer function. Only returned if output='zpk'.

sosndarray

Second-order sections representation of the IIR filter. Only returned if output=='sos'.

See also

cheb1ord, cheb1ap

Notes

The Chebyshev type I filter maximizes the rate of cutoff between the frequency response’s passband and stopband, at the expense of ripple in the passband and increased ringing in the step response.

Type I filters roll off faster than Type II (cheby2), but Type II filters do not have any ripple in the passband.

The equiripple passband has N maxima or minima (for example, a 5th-order filter has 3 maxima and 2 minima). Consequently, the DC gain is unity for odd-order filters, or -rp dB for even-order filters.

The 'sos' output parameter was added in 0.16.0.

Examples

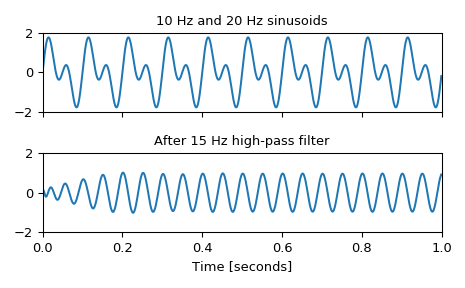
Design an analog filter and plot its frequency response, showing the critical points:

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> b, a = signal.cheby1(4, 5, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Chebyshev Type I frequency response (rp=5)')
>>> plt.xlabel('Frequency [radians / second]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.axhline(-5, color='green') # rp
>>> plt.show()

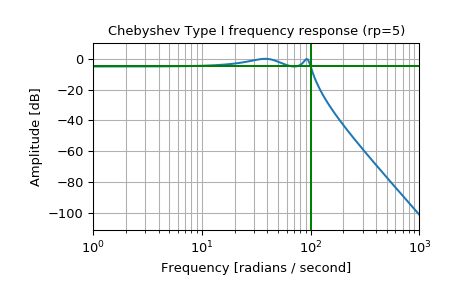
Generate a signal made up of 10 Hz and 20 Hz, sampled at 1 kHz

>>> t = np.linspace(0, 1, 1000, False)  # 1 second
>>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
>>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
>>> ax1.plot(t, sig)
>>> ax1.set_title('10 Hz and 20 Hz sinusoids')
>>> ax1.axis([0, 1, -2, 2])

Design a digital high-pass filter at 15 Hz to remove the 10 Hz tone, and apply it to the signal. (It’s recommended to use second-order sections format when filtering, to avoid numerical error with transfer function (ba) format):

>>> sos = signal.cheby1(10, 1, 15, 'hp', fs=1000, output='sos')
>>> filtered = signal.sosfilt(sos, sig)
>>> ax2.plot(t, filtered)
>>> ax2.set_title('After 15 Hz high-pass filter')
>>> ax2.axis([0, 1, -2, 2])
>>> ax2.set_xlabel('Time [seconds]')
>>> plt.tight_layout()
>>> plt.show()