scipy.linalg.lstsq

scipy.linalg.lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

Compute least-squares solution to equation Ax = b.

Compute a vector x such that the 2-norm |b - A x| is minimized.

Parameters

a(M, N) array_like

Left hand side matrix (2-D array).

b(M,) or (M, K) array_like

Right hand side matrix or vector (1-D or 2-D array).

condfloat, optional

Cutoff for ‘small’ singular values; used to determine effective rank of a. Singular values smaller than rcond * largest_singular_value are considered zero.

overwrite_abool, optional

Discard data in a (may enhance performance). Default is False.

overwrite_bbool, optional

Discard data in b (may enhance performance). Default is False.

check_finitebool, optional

Whether to check that the input matrices contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs.

lapack_driverstr, optional

Which LAPACK driver is used to solve the least-squares problem. Options are 'gelsd', 'gelsy', 'gelss'. Default ('gelsd') is a good choice. However, 'gelsy' can be slightly faster on many problems. 'gelss' was used historically. It is generally slow but uses less memory.

New in version 0.17.0.

Returns

x(N,) or (N, K) ndarray

Least-squares solution. Return shape matches shape of b.

residues(0,) or () or (K,) ndarray

Sums of residues, squared 2-norm for each column in b - a x. If rank of matrix a is < N or N > M, or 'gelsy' is used, this is a length zero array. If b was 1-D, this is a () shape array (numpy scalar), otherwise the shape is (K,).

rankint

Effective rank of matrix a.

s(min(M,N),) ndarray or None

Singular values of a. The condition number of a is abs(s[0] / s[-1]). None is returned when 'gelsy' is used.

Raises

LinAlgError

If computation does not converge.

ValueError

When parameters are wrong.

See also

optimize.nnls

linear least squares with non-negativity constraint

Examples

>>> from scipy.linalg import lstsq
>>> import matplotlib.pyplot as plt

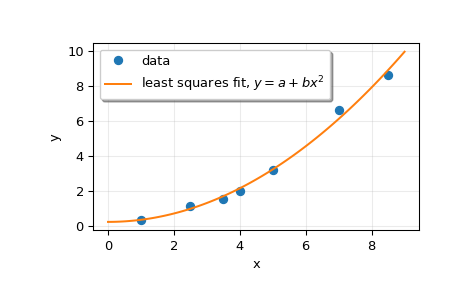
Suppose we have the following data:

>>> x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
>>> y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

We want to fit a quadratic polynomial of the form y = a + b*x**2 to this data. We first form the “design matrix” M, with a constant column of 1s and a column containing x**2:

>>> M = x[:, np.newaxis]**[0, 2]
>>> M
array([[  1.  ,   1.  ],
       [  1.  ,   6.25],
       [  1.  ,  12.25],
       [  1.  ,  16.  ],
       [  1.  ,  25.  ],
       [  1.  ,  49.  ],
       [  1.  ,  72.25]])

We want to find the least-squares solution to M.dot(p) = y, where p is a vector with length 2 that holds the parameters a and b.

>>> p, res, rnk, s = lstsq(M, y)
>>> p
array([ 0.20925829,  0.12013861])

Plot the data and the fitted curve.

>>> plt.plot(x, y, 'o', label='data')
>>> xx = np.linspace(0, 9, 101)
>>> yy = p[0] + p[1]*xx**2
>>> plt.plot(xx, yy, label='least squares fit, $y = a + bx^2$')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.grid(alpha=0.25)
>>> plt.show()