scipy.stats.siegelslopes

scipy.stats.siegelslopes(y, x=None, method='hierarchical')

Computes the Siegel estimator for a set of points (x, y).

siegelslopes implements a method for robust linear regression using repeated medians (see [1]) to fit a line to the points (x, y). The method is robust to outliers with an asymptotic breakdown point of 50%.

Parameters:

y : array_like

Dependent variable.

x : array_like or None, optional

Independent variable. If None, use arange(len(y)) instead.

method : {‘hierarchical’, ‘separate’}

If ‘hierarchical’, estimate the intercept using the estimated slope medslope (default option). If ‘separate’, estimate the intercept independent of the estimated slope. See Notes for details.

Returns:

medslope : float

Estimate of the slope of the regression line.

medintercept : float

Estimate of the intercept of the regression line.

See also

theilslopes

a similar technique without repeated medians

Notes

With n = len(y), compute m_j as the median of the slopes from the point (x[j], y[j]) to all other n-1 points. medslope is then the median of all slopes m_j. Two ways are given to estimate the intercept in [1] which can be chosen via the parameter method. The hierarchical approach uses the estimated slope medslope and computes medintercept as the median of y - medslope*x. The other approach estimates the intercept separately as follows: for each point (x[j], y[j]), compute the intercepts of all the n-1 lines through the remaining points and take the median i_j. medintercept is the median of the i_j.

The implementation computes n times the median of a vector of size n which can be slow for large vectors. There are more efficient algorithms (see [2]) which are not implemented here.

References

[1]	(1, 2, 3) A. Siegel, “Robust Regression Using Repeated Medians”, Biometrika, Vol. 69, pp. 242-244, 1982.

[2]	(1, 2) A. Stein and M. Werman, “Finding the repeated median regression line”, Proceedings of the Third Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 409-413, 1992.

Examples

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-5, 5, num=150)
>>> y = x + np.random.normal(size=x.size)
>>> y[11:15] += 10  # add outliers
>>> y[-5:] -= 7

Compute the slope and intercept. For comparison, also compute the least-squares fit with linregress:

>>> res = stats.siegelslopes(y, x)
>>> lsq_res = stats.linregress(x, y)

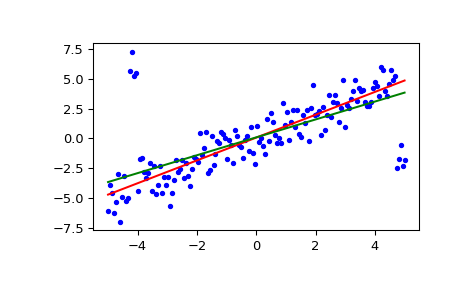
Plot the results. The Siegel regression line is shown in red. The green line shows the least-squares fit for comparison.

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, y, 'b.')
>>> ax.plot(x, res[1] + res[0] * x, 'r-')
>>> ax.plot(x, lsq_res[1] + lsq_res[0] * x, 'g-')
>>> plt.show()