scipy.signal.windows.general_cosine

scipy.signal.windows.general_cosine(M, a, sym=True)

Generic weighted sum of cosine terms window

Parameters:

M : int

Number of points in the output window

a : array_like

Sequence of weighting coefficients. This uses the convention of being centered on the origin, so these will typically all be positive numbers, not alternating sign.

sym : bool, optional

When True (default), generates a symmetric window, for use in filter design. When False, generates a periodic window, for use in spectral analysis.

References

[1]	A. Nuttall, “Some windows with very good sidelobe behavior,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, no. 1, pp. 84-91, Feb 1981. DOI:10.1109/TASSP.1981.1163506.

[2]	(1, 2) Heinzel G. et al., “Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows”, February 15, 2002 https://holometer.fnal.gov/GH_FFT.pdf

Examples

Heinzel describes a flat-top window named “HFT90D” with formula: [2]

\[w_j = 1 - 1.942604 \cos(z) + 1.340318 \cos(2z) - 0.440811 \cos(3z) + 0.043097 \cos(4z)\]

where

\[z = \frac{2 \pi j}{N}, j = 0...N - 1\]

Since this uses the convention of starting at the origin, to reproduce the window, we need to convert every other coefficient to a positive number:

>>> HFT90D = [1, 1.942604, 1.340318, 0.440811, 0.043097]

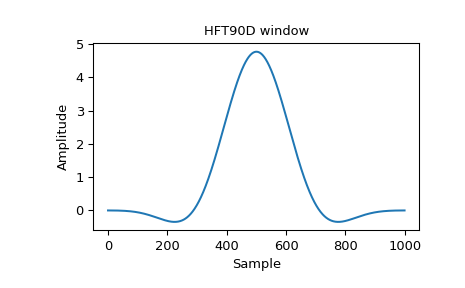
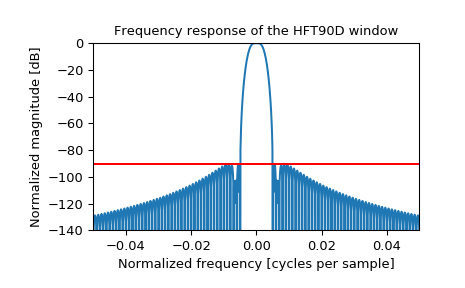
The paper states that the highest sidelobe is at -90.2 dB. Reproduce Figure 42 by plotting the window and its frequency response, and confirm the sidelobe level in red:

>>> from scipy.signal.windows import general_cosine
>>> from scipy.fftpack import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = general_cosine(1000, HFT90D, sym=False)
>>> plt.plot(window)
>>> plt.title("HFT90D window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 10000) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-50/1000, 50/1000, -140, 0])
>>> plt.title("Frequency response of the HFT90D window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")
>>> plt.axhline(-90.2, color='red')
>>> plt.show()